Значение двоичного кода – почему компьютеры работают с единицами и нулями

Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.

Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.

Подсчет в двоичном формате

В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.

Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.

Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.

Почему компьютеры используют двоичные файлы

Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.

Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.

Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.

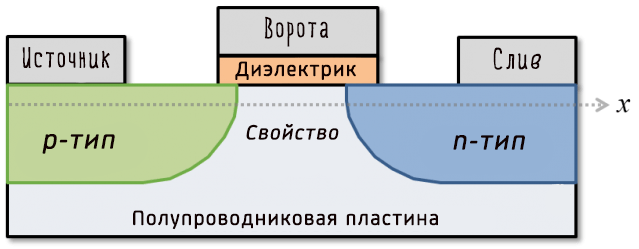
Вот схема типичного транзистора:

По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).

Почему только двоичная система

Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».

Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.

Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.

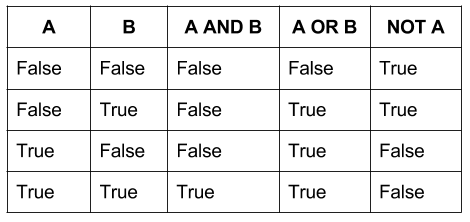
Таким образом, бинарная математика проще для компьютера, чем что-либо ещё. Двоичная логика легко преобразуется в двоичные системы, причем True и False соответствуют состояниям Вкл и Выкл .

Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.

Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.

Двоичная система счисления

Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.

Немного истории

Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.

Таблица и алфавит

Алфавит двоичной системы счисления состоит всего из двух знаков: 0 и 1 . Однако это нисколько не усложняет выполнение арифметических действий.

Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.

Так, чтобы перевести двоичное число в десятичное, необходимо найти значение его развернутой формы . Например:

100110₂ = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 38₁₀

Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:

Делимое	38	19	9	4	2
Делитель	2	2	2	2	2
Частное	19	9	4	2	1
Остаток	0	1	1	0	0

Для перевода в другие системы необходимо:

• Перевести двоичный код в десятичный.
• Выполнить деление десятичного числа на основание той системы, в которую требуется перевести.

Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:

Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

11001001₂ = 11 001 001 = 011 001 001 = 311₈

11001001₂ = 1100 1001 = С9₁₆

Представление двоичных чисел

В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.

Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.

Прямой код предполагает приписывание единицы в начале без изменений записи:

A > 0	Aпр = 0A	1010112; Aпр = 01010112
A ≤ 0	Aпр = 1|A|	-1010112; Aпр = 11010112

Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:

A > 0	Aобр = 0A	1010112; Aобр = 01010112
A ≤ 0	Aобр = 1 A	-1010112; Aобр = 10101002

Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:

A > 0	Aдоп = 0A	1010112; Aдоп = 01010112
A ≤ 0	Aдоп = 1 A + 1	-1010112; Aдоп = 10101012

Применение двоичной системы в информатике

Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.

Запись текстов двоичным кодом (Запись букв двоичным кодом)

Все символы и буквы могут быть закодированы при помощи восьми двоичных бит. Наиболее распространенными таблицами представления букв в двоичном коде являются ASCII и ANSI, их можно использовать для записи текстов в микропроцессорах. В таблицах ASCII и ANSI первые 128 символов совпадают. В этой части таблицы содержатся коды цифр, знаков препинания, латинские буквы верхнего и нижнего регистров и управляющие символы. Национальные расширения символьных таблиц и символы псевдографики содержатся в последних 128 кодах этих таблиц, поэтому русские тексты в операционных системах DOS и WINDOWS не совпадают.

При первом знакомстве с компьютерами и микропроцессорами может возникнуть вопрос — «как преобразовать текст в двоичный код?» Однако это преобразование является наиболее простым действием! Для этого нужно воспользоваться любым текстовым редактором. В том числе подойдет и простейшая программа notepad, входящая в состав операционной системы Windows. Подобные же редакторы присутствуют во всех средах программирования для языков, таких как СИ, Паскаль или Ява. Следует отметить, что наиболее распространенный текстовый редактор Word для простого преобразования текста в двоичный код не подходит. Этот тестовый редактор вводит огромное количество дополнительной информации, такой как цвет букв, наклон, подчеркивание, язык, на котором написана конкретная фраза, шрифт.

Следует отметить, что на самом деле комбинация нулей и единиц, при помощи которых кодируется текстовая информация двоичным кодом не является, т.к. биты в этом коде не подчиняются законам двоичной системы счисления. Однако в Интернете поисковая фраза «представление букв в двоичном коде» является самой распространенной. В таблице 1 приведено соответствие двоичных кодов буквам латинского алфавита. Для краткости записи в этой таблице последовательность нулей и единиц представлена в десятичном и шестнадцатеричном кодах.

Таблица 1 Таблица представления латинских букв в двоичном коде (ASCII)

Десятичный код	Шестнадцатеричный код	Отображаемый символ	Значение
0	00	NUL
1	01	☺	(слово управления дисплеем)
2	02	☻	(Первое передаваемое слово)
3	03	♥	ETX (Последнее слово передачи)
4	04	♦	EOT (конец передачи)
5	05	♣	ENQ (инициализация)
6	06	♠	ACK (подтверждение приема)
7	07	•	BEL
8	08	◘	BS
9	09	○	HT (горизонтальная табуляция
10	0A	◙	LF (перевод строки)
11	0B	♂	VT (вертикальная табуляция)
12	0С	♀	FF (следующая страница)
13	0D	♪	CR (возврат каретки)
14	0E	♫	SO (двойная ширина)
15	0F	☼	SI (уплотненная печать)
16	10	►	DLE
17	11	◄	DC1
18	12	↕	DC2 (отмена уплотненной печати)
19	13	‼	DC3 (готовность)
20	14	¶	DC4 (отмена двойной ширины)
21	15	§	NAC (неподтверждение приема)
22	16	▬	SYN
23	17	↨	ETB
24	18	↑	CAN
25	19	↓	EM
26	1A	→	SUB
27	1B	←	ESC (начало управл. послед.)
28	1C	∟	FS
29	1D	↔	GS
30	1E	▲	RS
31	1F	▼	US
32	20	Пробел
33	21	!	Восклицательный знак
34	22	«	Угловая скобка
35	23	#	Знак номера
36	24	$	Знак денежной единицы (доллар)
37	25	%	Знак процента
38	26	&	Амперсанд
39	27	‘	Апостроф
40	28	(	Открывающая скобка
41	29	)	Закрывающая скобка
42	2A	*	Звездочка
43	2B	+	Знак плюс
44	2C	,	Запятая
45	2D	—	Знак минус
46	2E	.	Точка
47	2F	/	Дробная черта
48	30	0	Цифра ноль
49	31	1	Цифра один
50	32	2	Цифра два
51	33	3	Цифра три
52	34	4	Цифра четыре
53	35	5	Цифра пять
54	36	6	Цифра шесть
55	37	7	Цифра семь
56	38	8	Цифра восемь
57	39	9	Цифра девять
58	3A	:	Двоеточие
59	3B	;	Точка с запятой
60	3C	Знак больше
63	3F	?	Знак вопрос
64	40	@	Коммерческое эт
65	41	A	Прописная латинская буква А
66	42	B	Прописная латинская буква B
67	43	C	Прописная латинская буква C
68	44	D	Прописная латинская буква D
69	45	E	Прописная латинская буква E
70	46	F	Прописная латинская буква F
71	47	G	Прописная латинская буква G
72	48	H	Прописная латинская буква H
73	49	I	Прописная латинская буква I
74	4A	J	Прописная латинская буква J
75	4B	K	Прописная латинская буква K
76	4C	L	Прописная латинская буква L
77	4D	M	Прописная латинская буква
78	4E	N	Прописная латинская буква N
79	4F	O	Прописная латинская буква O
80	50	P	Прописная латинская буква P
81	51	Q	Прописная латинская буква
82	52	R	Прописная латинская буква R
83	53	S	Прописная латинская буква S
84	54	T	Прописная латинская буква T
85	55	U	Прописная латинская буква U
86	56	V	Прописная латинская буква V
87	57	W	Прописная латинская буква W
88	58	X	Прописная латинская буква X
89	59	Y	Прописная латинская буква Y
90	5A	Z	Прописная латинская буква Z
91	5B	[	Открывающая квадратная скобка
92	5C	\	Обратная черта
93	5D	]	Закрывающая квадратная скобка
94	5E	^	«Крышечка»
95	5	_	Символ подчеркивания
96	60	`	Апостроф
97	61	a	Строчная латинская буква a
98	62	b	Строчная латинская буква b
99	63	c	Строчная латинская буква c
100	64	d	Строчная латинская буква d
101	65	e	Строчная латинская буква e
102	66	f	Строчная латинская буква f
103	67	g	Строчная латинская буква g
104	68	h	Строчная латинская буква h
105	69	i	Строчная латинская буква i
106	6A	j	Строчная латинская буква j
107	6B	k	Строчная латинская буква k
108	6C	l	Строчная латинская буква l
109	6D	m	Строчная латинская буква m
110	6E	n	Строчная латинская буква n
111	6F	o	Строчная латинская буква o
112	70	p	Строчная латинская буква p
113	71	q	Строчная латинская буква q
114	72	r	Строчная латинская буква r
115	73	s	Строчная латинская буква s
116	74	t	Строчная латинская буква t
117	75	u	Строчная латинская буква u
118	76	v	Строчная латинская буква v
119	77	w	Строчная латинская буква w
120	78	x	Строчная латинская буква x
121	79	y	Строчная латинская буква y
122	7A	z	Строчная латинская буква z
123	7B	<	Открывающая фигурная скобка
124	7С	|	Вертикальная черта
125	7D	>	Закрывающая фигурная скобка
126	7E	Тильда
127	7F	⌂

В классическом варианте таблицы символов ASCII нет русских букв и она состоит из . Однако в дальнейшем эта таблица была расширена до и в старших 128 строках появились русские буквы в двоичном коде и символы псевдографики. В общем случае во второй части размещены национальные алфавиты разных стран и русские буквы там просто один из возможных наборов (855) там может быть французская (863), немецкая (1141) или греческая (737) таблица. В таблице 2 приведен пример представления русских букв в двоичном коде.

Таблица 2. Таблица представления русских букв в двоичном коде (ASCII)

Десятичный код	Шестнадцатеричный код	Отображаемый символ	Значение
128	80	А	Прописная русская буква А
129	81	Б	Прописная русская буква Б
130	82	В	Прописная русская буква В
131	83	Г	Прописная русская буква Г
132	84	Д	Прописная русская буква Д
133	85	Е	Прописная русская буква Е
134	86	Ж	Прописная русская буква Ж
135	87	З	Прописная русская буква З
136	88	И	Прописная русская буква И
137	89	Й	Прописная русская буква Й
138	8A	К	Прописная русская буква К
139	8B	Л	Прописная русская буква Л
140	8C	М	Прописная русская буква М
141	8D	Н	Прописная русская буква Н
142	8E	О	Прописная русская буква О
143	8F	П	Прописная русская буква П
144	90	Р	Прописная русская буква Р
145	91	С	Прописная русская буква С
146	92	Т	Прописная русская буква Т
147	93	У	Прописная русская буква У
148	94	Ф	Прописная русская буква Ф
149	95	Х	Прописная русская буква Х
150	96	Ц	Прописная русская буква Ц
151	97	Ч	Прописная русская буква Ч
152	98	Ш	Прописная русская буква Ш
153	99	Щ	Прописная русская буква Щ
154	9A	Ъ	Прописная русская буква Ъ
155	9B	Ы	Прописная русская буква Ы
156	9C	Ь	Прописная русская буква Ь
157	9D	Э	Прописная русская буква Э
158	9E	Ю	Прописная русская буква Ю
159	9F	Я	Прописная русская буква Я
160	A0	а	Строчная русская буква а
161	A1	б	Строчная русская буква б
162	A2	в	Строчная русская буква в
163	A3	г	Строчная русская буква г
164	A4	д	Строчная русская буква д
165	A5	е	Строчная русская буква е
166	A6	ж	Строчная русская буква ж
167	A7	з	Строчная русская буква з
168	A8	и	Строчная русская буква и
169	A9	й	Строчная русская буква й
170	AA	к	Строчная русская буква к
171	AB	л	Строчная русская буква л
172	AC	м	Строчная русская буква м
173	AD	н	Строчная русская буква н
174	AE	о	Строчная русская буква о
175	AF	п	Строчная русская буква п
176	B0	░
177	B1	▒
178	B2	▓
179	B3	│	Символ псевдографики
180	B4	┤	Символ псевдографики
181	B5	╡	Символ псевдографики
182	B6	╢	Символ псевдографики
183	B7	╖	Символ псевдографики
184	B8	╕	Символ псевдографики
185	B9	╣	Символ псевдографики
186	BA	║	Символ псевдографики
187	BB	╗	Символ псевдографики
188	BC	╝	Символ псевдографики
189	BD	╜	Символ псевдографики
190	BE	╛	Символ псевдографики
191	BF	┐	Символ псевдографики
192	C0	└	Символ псевдографики
193	C1	┴	Символ псевдографики
194	C2	┬	Символ псевдографики
195	C3	├	Символ псевдографики
196	C4	─	Символ псевдографики
197	C5	┼	Символ псевдографики
198	C6	╞	Символ псевдографики
199	C7	╟	Символ псевдографики
200	C8	╚	Символ псевдографики
201	C9	╔	Символ псевдографики
202	CA	╩	Символ псевдографики
203	CB	╦	Символ псевдографики
204	CC	╠	Символ псевдографики
205	CD	═	Символ псевдографики
206	CE	╬	Символ псевдографики
207	CF	╧	Символ псевдографики
208	D0	╨	Символ псевдографики
209	D1	╤	Символ псевдографики
210	D2	╥	Символ псевдографики
211	D3	╙	Символ псевдографики
212	D4	╘	Символ псевдографики
213	D5	╒	Символ псевдографики
214	D6	╓	Символ псевдографики
215	D7	╫	Символ псевдографики
216	D8	╪	Символ псевдографики
217	D9	┘	Символ псевдографики
218	DA	┌	Символ псевдографики
219	DB	█
220	DC	▄
221	DD	▌
222	DE	▐
223	DF	▀
224	E0	р	Строчная русская буква р
225	E1	с	Строчная русская буква с
226	E2	т	Строчная русская буква т
227	E3	у	Строчная русская буква у
228	E4	ф	Строчная русская буква ф
229	E5	х	Строчная русская буква х
230	E6	ц	Строчная русская буква ц
231	E7	ч	Строчная русская буква ч
232	E8	ш	Строчная русская буква ш
233	E9	щ	Строчная русская буква щ
234	EA	ъ	Строчная русская буква ъ
235	EB	ы	Строчная русская буква ы
236	EC	ь	Строчная русская буква ь
237	ED	э	Строчная русская буква э
238	EE	ю	Строчная русская буква ю
239	EF	я	Строчная русская буква я
240	F0	Ё	Прописная русская буква Ё
241	F1	ё	Строчная русская буква ё
242	F2	Є
243	F3	є
244	F4	Ї
245	F5	Ї
246	F6	Ў
247	F7	ў
248	F8	°	Знак градуса
249	F9	∙	Знак умножения (точка)
250	FA	·
251	FB	√	Радикал (взятие корня)
252	FC	№	Знак номера
253	FD	¤	Знак денежной единицы (рубль)
254	FE	■
255	FF

При записи текстов кроме двоичных кодов, непосредственно отображающих буквы, применяются коды, обозначающие переход на новую строку и возврат курсора (возврат каретки) на нулевую позицию строки. Эти символы обычно применяются вместе. Их двоичные коды соответствуют десятичным числам — 10 (0A) и 13 (0D). В качестве примера ниже приведен участок текста данной страницы (дамп памяти). На этом участке записан ее первый абзац. Для отображения информации в дампе памяти применен следующий формат:

• в первой колонке записан двоичный адрес первого байта строки
• в следующи шестнадцати колонках записаны байты, содержащиеся в текстовом файле. Для более удобного определения номера байта после восьмой колонки проведена вертикальная линия. Байты, для краткости записи, представлены в шестнадцатеричном коде.
• в последней колонке эти же байты представлены в виде отображаемых буквенных символов

В приведенном примере видно, что первая строка текста занимает 80 байт. Первый байт 82 соответствует букве ‘В’. Второй байт E1 соответствует букве ‘с’. Третий байт A5 соответствует букве ‘е’. Следующий байт 20 отображает пустой промежуток между словами (пробел) ‘ ‘. 81 и 82 байты содержат символы возврата каретки и перевода строки 0D 0A. Эти символы мы находим по двоичному адресу 00000050: Следующая строка исходного текста не кратна 16 (ее длина равна 76 буквам), поэтому для того, чтобы найти ее конец потребуется сначала найти строку 000000E0: и от нее отсчитать девять колонок. Там снова записаны байты возврата каретки и перевода строки 0D 0A. Остальной текст анализируется точно таким же образом.

Дата последнего обновления файла 04.12.2018