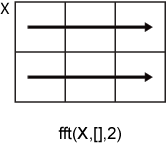
Discrete Fourier Transform

The discrete Fourier transform, or DFT, is the primary tool of digital signal processing. The foundation of the product is the fast Fourier transform (FFT), a method for computing the DFT with reduced execution time. Many of the toolbox functions (including Z -domain frequency response, spectrum and cepstrum analysis, and some filter design and implementation functions) incorporate the FFT.

The MATLAB® environment provides the functions fft and ifft to compute the discrete Fourier transform and its inverse, respectively. For the input sequence x and its transformed version X (the discrete-time Fourier transform at equally spaced frequencies around the unit circle), the two functions implement the relationships

X ( k + 1 ) = ∑ n = 0 N — 1 x ( n + 1 ) W N k n

x ( n + 1 ) = 1 N ∑ k = 0 N — 1 X ( k + 1 ) W N — k n .

In these equations, the series subscripts begin with 1 instead of 0 because of the MATLAB vector indexing scheme, and

W N = e — j 2 π / N .

Note The MATLAB convention is to use a negative j for the fft function. This is an engineering convention; physics and pure mathematics typically use a positive j .

fft , with a single input argument, x , computes the DFT of the input vector or matrix. If x is a vector, fft computes the DFT of the vector; if x is a rectangular array, fft computes the DFT of each array column.

For example, create a time vector and signal:

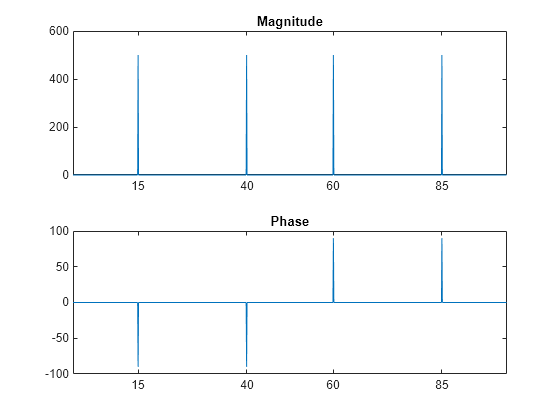
Compute the DFT of the signal and the magnitude and phase of the transformed sequence. Decrease round-off error when computing the phase by setting small-magnitude transform values to zero.

To plot the magnitude and phase in degrees, type the following commands:

A second argument to fft specifies a number of points n for the transform, representing DFT length:

In this case, fft pads the input sequence with zeros if it is shorter than n , or truncates the sequence if it is longer than n . If n is not specified, it defaults to the length of the input sequence. Execution time for fft depends on the length, n , of the DFT it performs; see the fft reference page for details about the algorithm.

Note The resulting FFT amplitude is A*n/2 , where A is the original amplitude and n is the number of FFT points. This is true only if the number of FFT points is greater than or equal to the number of data samples. If the number of FFT points is less, the FFT amplitude is lower than the original amplitude by the above amount.

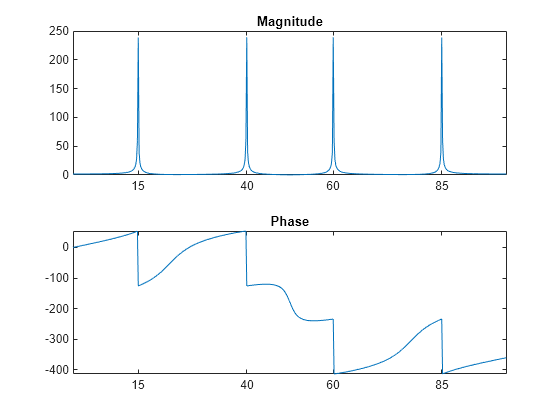
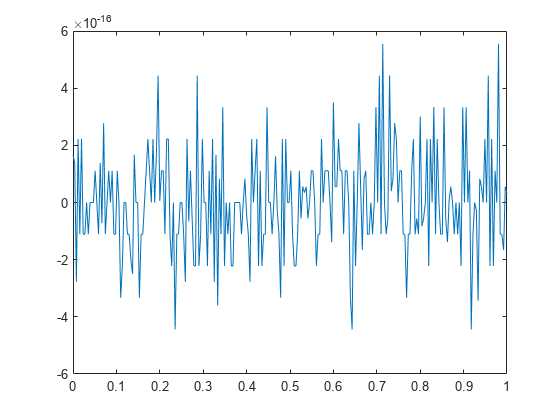
The inverse discrete Fourier transform function ifft also accepts an input sequence and, optionally, the number of desired points for the transform. Try the example below; the original sequence x and the reconstructed sequence are identical (within rounding error).

This toolbox also includes functions for the two-dimensional FFT and its inverse, fft2 and ifft2 . These functions are useful for two-dimensional signal or image processing. The goertzel function, which is another algorithm to compute the DFT, also is included in the toolbox. This function is efficient for computing the DFT of a portion of a long signal.

It is sometimes convenient to rearrange the output of the fft or fft2 function so the zero frequency component is at the center of the sequence. The function fftshift moves the zero frequency component to the center of a vector or matrix.

Документация

Быстрое преобразование Фурье

Синтаксис

Описание

Y = fft( X ) вычисляет дискретное преобразование Фурье (DFT) X использование алгоритма быстрого преобразования Фурье (FFT).

Если X вектор, затем fft(X) возвращает преобразование Фурье вектора.

Если X матрица, затем fft(X) обрабатывает столбцы X как векторы и возвращает преобразование Фурье каждого столбца.

Если X многомерный массив, затем fft(X) обрабатывает значения вдоль первого измерения массива, размер которого не равняется 1 как векторы и возвращает преобразование Фурье каждого вектора.

Y = fft( X , n ) возвращает n — укажите ДПФ, Если никакое значение не задано, Y одного размера с X .

Если X вектор и длина X меньше n , затем X дополнен конечными нулями к длине n .

Если X вектор и длина X больше n , затем X является усеченным к длине n .

Если X матрица, затем каждый столбец обработан как в векторном случае.

Если X многомерный массив, затем первое измерение массива, размер которого не равняется 1, обработано как в векторном случае.

Y = fft( X , n , dim ) возвращает преобразование Фурье по измерению dim . Например, если X матрица, затем fft(X,n,2) возвращает преобразование Фурье n значений каждой строки.

Примеры

Сигнал с шумом

Использование преобразования Фурье, для нахождения частотных составляющих сигнала, содержащего шум.

Задайте параметры сигнала с частотой дискретизации 1 кГц и длительностью сигнала 1,5 секунд.

Сформируйте сигнал, содержащий синусоиду на 50 Гц амплитуды 0.7 и синусоиду на 120 Гц амплитуды 1.

Повредите сигнал с нулевым средним белым шумом с отклонением 4.

Постройте сигнал с шумом во временном интервале. Это затрудняет, чтобы идентифицировать частотные составляющие путем рассмотрения X(t) сигнала .

Вычислите преобразование Фурье сигнала.

Вычисление двухстороннего спектра P2 . Затем вычислите односторонний спектр P1 на основе P2 и четная длина сигнала L .

Задайте частотный диапазон f и постройте односторонний амплитудный спектр P1 . Амплитуды не точно в 0,7 и 1, как ожидалось, из-за добавленного шума. В среднем более длинные сигналы производят лучшие приближения частоты.

Теперь возьмите преобразование Фурье исходного, неповрежденного сигнала и получите точные амплитуды, 0.7 и 1.0.

Гауссов импульс

Преобразуйте Гауссов импульс от временного интервала до частотного диапазона.

Задайте параметры сигнала и Гауссов импульс, X .

Постройте импульс во временном интервале.

Использовать fft функционируйте, чтобы преобразовать сигнал в частотный диапазон, сначала определить новую входную длину, которая является следующей степенью 2 от исходной длины сигнала. Это заполнит X сигнала с конечными нулями для того, чтобы улучшать производительность fft .

Преобразуйте Гауссов импульс в частотный диапазон.

Задайте частотный диапазон и постройте уникальные частоты.

Волны косинуса

Сравните волны косинуса во временном интервале и частотном диапазоне.

Задайте параметры сигнала с частотой дискретизации 1 кГц и длительностью сигнала 1 секунды.

Создайте матрицу, где каждая строка представляет волну косинуса масштабированной частотой. Результат, X , 3 1000 матрица. Первая строка имеет частоту волны 50, вторая строка имеет частоту волны 150, и третья строка имеет частоту волны 300.

Постройте первые 100 записей из каждой строки X на одной фигуре в порядке и сравнивают их частоты.

В целях эффективности алгоритма, fft позволяет вам заполнять вход конечными нулями. В этом случае заполните каждую строку X с нулями так, чтобы длина каждой строки была следующей более высокой степенью 2 от текущей длины. Задайте новую длину с помощью nextpow2 функция.

Задайте dim аргумент, чтобы использовать fft вдоль строк X , то есть, для каждого сигнала.

Вычислите преобразование Фурье сигналов.

Вычислите двусторонний спектр и односторонний спектр каждого сигнала.

В частотном диапазоне постройте односторонний амплитудный спектр для каждой строки на одной фигуре.

Входные параметры

X — Входной массив
вектор | матрица | многомерный массив

Входной массив, заданный как векторный, матричный или многомерный массив.

Если X пустая матрица 0 на 0, затем fft(X) возвращает пустую матрицу 0 на 0.

Типы данных: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
Поддержка комплексного числа: Да

n — Преобразуйте длину
[] (значение по умолчанию) | неотрицательный целочисленный скаляр

Преобразуйте длину в виде [] или неотрицательный целочисленный скаляр. Определение положительного целочисленного скаляра для длины преобразования может увеличить эффективность fft . Длина обычно задается как степень 2 или значение, которое может быть включено в продукт маленьких простых чисел. Если n меньше длины сигнала, затем fft игнорирует остающиеся значения сигналов мимо n запись th и возвращает усеченный результат. Если n 0 , затем fft возвращает пустую матрицу.

Пример: n = 2^nextpow2(size(X,1))

Типы данных: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр

Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.

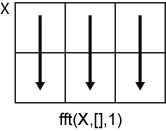
fft(X,[],1) действует вдоль столбцов X и возвращает преобразование Фурье каждого столбца.

fft(X,[],2) действует вдоль строк X и возвращает преобразование Фурье каждой строки.

Если dim больше ndims(X) , затем fft(X,[],dim) возвращает X . Когда n задан, fft(X,n,dim) клавиатуры или обрезают X к длине n по измерению dim .

Типы данных: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

Выходные аргументы

Y — Представление частотного диапазона
вектор | матрица | многомерный массив

Представление частотного диапазона, возвращенное как вектор, матрица или многомерный массив.

Если X имеет тип single , затем fft исходно вычисляет в одинарной точности и Y также имеет тип single . В противном случае, Y возвращен как тип double .

Размер Y следующие:

Для Y = fft(X) или Y = fft(X,[],dim) , размер Y равно размеру X .

Для Y = fft(X,n,dim) , значение size(Y,dim) равно n , в то время как размер всех других размерностей остается как в X .

Если X действительно, затем Y сопряжен симметричный, и количество уникальных точек в Y ceil((n+1)/2) .

Типы данных: double | single

Больше о

Дискретное преобразование Фурье вектора

Y = fft(X) и X = ifft(Y) реализуйте преобразование Фурье и обратное преобразование Фурье, соответственно. Для X и Y из длины n , эти преобразования определяются следующим образом:

Y ( k ) = ∑ j = 1 n X ( j ) W n ( j − 1 ) ​ ( k − 1 ) X ( j ) = 1 n ∑ k = 1 n Y ( k ) W n − ( j − 1 ) ​ ( k − 1 ) ,

W n = e ( − 2 π i ) / n

один из корней из единицы n.

Советы

Время выполнения для fft зависит от длины преобразования. Преобразуйте длины, которые имеют только малые простые множители, значительно быстрее, чем те, которые являются главными или имеют большие простые множители.

Для большинства значений n , ДПФ с реальным входом требуют примерно половины времени вычисления ДПФ с комплексным входом Однако когда n имеет большие простые множители, существует минимальное различие в скорости.

Можно потенциально увеличить скорость fft использование служебной функции, fftw . Эти средства управления функцией оптимизация алгоритма использовались для расчета БПФ конкретного размера и размерности.

Алгоритмы

Функции БПФ ( fft , fft2 , fftn , ifft , ifft2 , ifftn ) основаны на библиотеке под названием [1]FFTW [2].

Ссылки

[2] Frigo, M. и С. Г. Джонсон. fftw: Адаптивная Программная архитектура для БПФ”. Продолжения Международной конференции по вопросам Акустики, Речи и Обработки сигналов. Издание 3, 1998, стр 1381-1384.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

Для ограничений, связанных с данными переменного размера, смотрите Измеряющие Переменную Ограничения для Генерации кода Функций Тулбокса (MATLAB Coder) .

Для MEX выход MATLAB ® Coder™ пользуется библиотекой, которой MATLAB пользуется для Алгоритмов бпф. Для автономного кода C/C++, по умолчанию, генератор кода производит код для Алгоритмов бпф вместо того, чтобы произвести вызовы библиотеки FFT. Чтобы сгенерировать вызовы определенной установленной библиотеки FFTW, обеспечьте класс коллбэка библиотеки FFT. Для получения дополнительной информации о классе коллбэка библиотеки FFT, смотрите coder.fftw.StandaloneFFTW3Interface (MATLAB Coder) .

Для симуляции блока MATLAB Function программное обеспечение симуляции пользуется библиотекой, которой MATLAB пользуется для Алгоритмов бпф. Для генерации кода C/C++, по умолчанию, генератор кода производит код для Алгоритмов бпф вместо того, чтобы произвести вызовы библиотеки FFT. Чтобы сгенерировать вызовы определенной установленной библиотеки FFTW, обеспечьте класс коллбэка библиотеки FFT. Для получения дополнительной информации о классе коллбэка библиотеки FFT, смотрите coder.fftw.StandaloneFFTW3Interface (MATLAB Coder) .

Используя Заменяющую библиотеку кода (CRL), можно сгенерировать оптимизированный код, который работает на процессорах ARM ® Cortex ® -A с Неоновым расширением. Чтобы сгенерировать этот оптимизированный код, необходимо установить Embedded Coder ® Support Package для процессоров ARM Cortex-A (Пакет Поддержки Embedded Coder для процессоров ARM Cortex-A) . Сгенерированный код для ARM Cortex-A пользуется библиотекой Ne10. Для получения дополнительной информации см. Условия Ne10 для функций MATLAB, чтобы Поддержать процессоры ARM Cortex-A (Пакет Поддержки Embedded Coder для процессоров ARM Cortex-A) .

Используя Заменяющую библиотеку кода (CRL), можно сгенерировать оптимизированный код, который работает на процессорах ARM Cortex-M . Чтобы сгенерировать этот оптимизированный код, необходимо установить Пакет Поддержки Embedded Coder для процессоров ARM Cortex-M (Пакет Поддержки Embedded Coder для процессоров ARM Cortex-M) . Сгенерированный код для ARM Cortex-M пользуется библиотекой CMSIS. Для получения дополнительной информации см. Условия CMSIS для функций MATLAB, чтобы Поддержать процессоры ARM Cortex-M (Пакет Поддержки Embedded Coder для процессоров ARM Cortex-M) .

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Указания и ограничения по применению:

Выход Y является всегда комплексным, даже если все мнимые части являются нулем.

Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox) .

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Указания и ограничения по применению:

Для распределенных массивов, вместо того, чтобы использовать параллельный Алгоритм бпф, fft собирает векторы на одном рабочем, чтобы выполнить главные БПФ длины. Для больших БПФ вектора главной длины могут закончиться ошибки из памяти.

Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox) .