Как написан калькулятор windows

Одна из задач, задаваемых студентам по программированию, это создание калькулятора. Раскрою вам небольшой секрет: немало практических, курсовых и лабораторных работ на C++, C# и Java можно и не делать самостоятельно – есть готовые решения в сети. Однако, я был несколько удивлен, что для такого распространенного задания, как визуальный калькулятор на C++ нет такого готового решения. Ну что ж, нет, так нет, давайте напишем его сами.

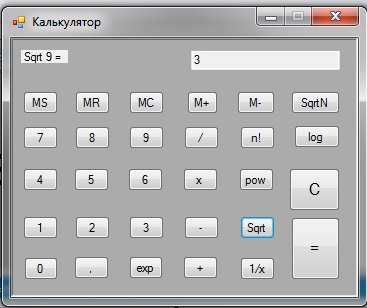
Итак, как в большинстве проектов, все начинается с создания приложения Windows Forms, а уже в нем – с редактирования формы. У нас получилась вот такая:

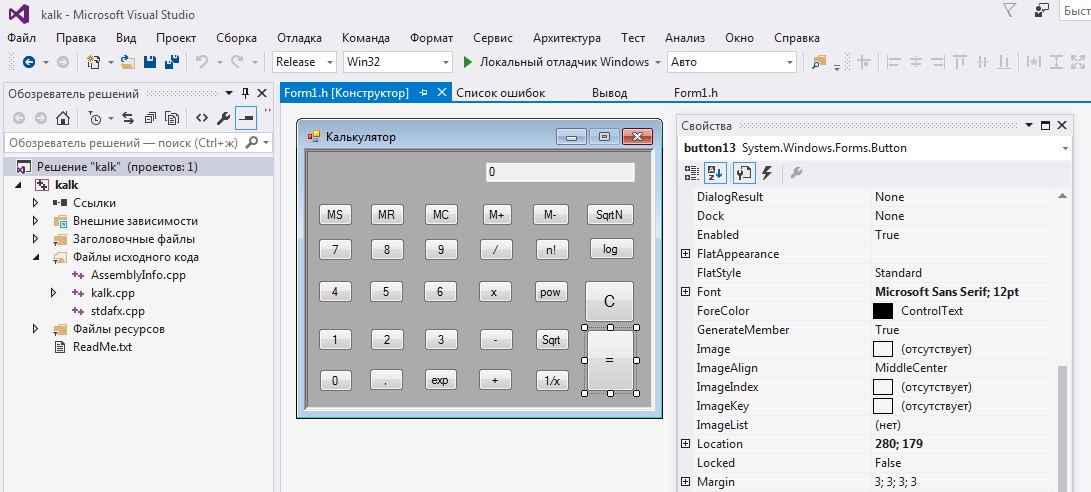
Проект для VS2015

В чем будем считать и хранить числа? Я выбрал тип double – точности его нам вполне хватит; это все же студенческая работа, а не для точных инженерных расчетов. Дальше определимся с тем, сколько чисел и операций будем хранить в памяти. Предположим, штук двадцать: тогда надо создать два массива – один для чисел, а другой для операций между ними.

Почему мы воспользовались указателями, а не просто создали глобальные переменные за пределами windows forms? Дело в том, что, использование глобальных переменных – это плохой тон при программировании, и очень часто преподаватели против данной практики студентов.

В нашей программе будут три основных метода: vvod — принимает цифру (нажатую кнопку) в качестве аргумента и добавляет её к числу. ravno — нажатие на кнопку равно — все считает, ravno2 — это нажатие на кнопку знака. Факториал, деление единицы на число и корень квадратные — там реализуются методы сразу при нажатии все обрабатывается.

Добавим также флаг для памяти:

И еще систему флагов:

Вот, например, как у нас будет выглядеть метод vvod():

Здесь мы проверяем, какая клавиша в нашем калькуляторе была нажата перед этим – цифра, арифметическая операция или знак равно. Далее получаем из текстбокса значение, конвертируем предыдущее из массива, конкатенируем строки, потом обратно в double и обновляем значение массива. Также в этом методе мы проверяем длину числа – мы поставили ограничение на 10 знаков.

Обработка кнопки равно – то есть метод вычисления – также не представляет сложности. Пользуясь оператором ветвления switch перебираем все варианты.

Также реализуем собственный класс для обработки ошибок. Зачем это надо? Дело в том, что мы оперируем с числами типа double, а они не выбрасывают некоторые стандартные исключения, например – деление на ноль. Также мы предусмотрим обработку переполнения и вычисления квадратного корня из отрицательного числа. На вход конструкторов этого класса будем принимать пару чисел. Выводятся ошибки при:

1. взятии корня четной степени из отрицательного числа
2. логарифмировании отрицательного числа и нуля
3. делении на нуль.
4. переполнении (калькулятор все же не бесконечный)

Также не забудем и обработку клавиши запятой. Для этого проверяем, есть ли она уже во введённом числе:

Вот такие основные моменты надо знать для написания данной программы. Ну а если вы не можете самостоятельно написать визуальный калькулятор на C++, то обратитесь ко мне. Актуальную цену за архив с готовой программой и исходниками с подробными комментариями в настоящий моент 500 рублей. Это будет проект в Visual Studio C++ 2010 — он откроется в любой другой версии студии не ниже 2010. Также есть проект для Visual Studio 2015.

Мой калькулятор реализует все основные функции: сложение, вычитание, деление, умножение, факториал, возведение в степень, извлечение квадратного корня, вычисление 1/x, функции памяти (занести в память, вывести содержимое памяти, очистить память).

Добавились новые функции в калькуляторе. А именно:

• Извлечение корня четной и нечетной степени из числа
• Вычисление логарифма по любому основанию
• Вычисление экспоненты

Если вам требуется реализация других функций, то это делается за отдельную плату. Пишите на почту up777up@yandex.ru, стучитесь vk.com/idup7, @upreadru или по другим контактам.

Автор этого материала — я — Пахолков Юрий. Я оказываю услуги по написанию программ на языках Java, C++, C# (а также консультирую по ним) и созданию сайтов. Работаю с сайтами на CMS OpenCart, WordPress, ModX и самописными. Кроме этого, работаю напрямую с JavaScript, PHP, CSS, HTML — то есть могу доработать ваш сайт или помочь с веб-программированием. Пишите сюда.

статьи IT, си плюс плюс, visual studio, калькулятор

Как написать калькулятор, подобный калькулятору в Windows

Написать калькулятор, подобный калькулятору Windows
Народ срочно нужна помощь!!Горит курсовая я я так и не успел сделать 1 задание из 3.Нужно написать.

Как создать подобный калькулятор
Как создать подобный калькулятор Вот такой

Как создать подобный калькулятор?
Целый день пробую не в какую, пробовал элемент output тоже самое. Вот ссылка .

Как сделать подобный калькулятор
Здравствуйте, подскажите, может кто видел код подобного калькулятора.

странно в 2005 не должно быть, так как в 2005 студии используется framework 2.0, а WPF появился с выходом framework 3.0

Я решил написать свою IDE, вот мой код, добавьте в него код как в vusial studio 2010.

Про 2005 я и правда ошибся

вы анекдот про Неуловимого Джо слышали?

Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь или здесь.

Как написать подобный язык программирования?
Это даже скорее не язык программирования, я реализация типовых функций. Я хочу реализовать грубо.

Создать форму, визуально идентичную калькулятору Windows
Как создать форму визуальноидентичную калькулятору операционной системы Windows и реализовать ввод.

Как добавить к калькулятору скобки
Помогите добавить к калькулятору скобки, вот код C # using System; using.

Добавить 5 кнопок к калькулятору, как это сделать?
Добрый вечер! Возник вопрос. Создал калькулятор. Добавил все необходимые функции. Но надо добавить.

Пишем «калькулятор» на C#. Часть I. Вычисление значения, производная, упрощение, и другие гуси

Калькулятор у нас почему-то ассоциируется с чем-то, что должен написать каждый новичок. Возможно потому, что исторически компьютеры с той целью и создавались, чтобы считать. Но мы будем писать непростой калькулятор, не sympy конечно, но чтобы умел базовые алгебраические операции, типа дифференциирования, симплификации, а также фичи типа компиляции для ускорения вычислений.

Сборка выражения

Что такое «выражение»?

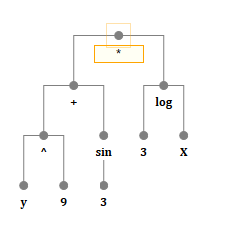
Конечно, это не строка. Довольно очевидно, что математическая формула — это либо дерево, либо стек, и здесь мы остановимся на первом. То есть каждая нода, каждый узел этого дерева, это какая-то операция, переменная, либо константа.

Операция — это либо функция, либо оператор, в принципе, примерно одно и то же. Ее дети — аргументы функции (оператора).

Иерархия классов в вашем коде

Разумеется, реализация может быть любой. Однако идея в том, что если ваше дерево состоит только из узлов и листьев, то они бывают разными. Поэтому я называю эти «штуки» — сущностями. Поэтому верхним классом у нас будет абстрактный класс Entity.

А также будет четыре класса-наследника: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.

Как построить выражение?

Для начала мы будем строить выражение в коде, то есть

Если объявить пустой класс VariableEntity, то такой код выкинет вам ошибку, мол не знает как умножать и суммировать.

Переопределение операторов

Очень важная и полезная фича большинства языков, позволяя кастомизировать выполнение арифметических операций. Синтаксически реализуется по-разному в зависимости от языка. Например, реализация в C#

(Не)явное приведение типов

В компилируемых языках типа C# такая штука обычно присутствует и позволяет без дополнительного вызова myvar.ToAnotherType() привести тип, если необходимо. Так, например, было бы удобно писать

Подвешивание

Класс Entity имеет поле Children — это просто список Entity, которые являются аргументами для данной сущности.

Когда у нас вызывается функция или оператор, нам стоит создать новую сущность, и в ее дети положить то, от чего вызывается функция или оператор. К примеру, сумма по идее должна выглядить примерно так:

То есть теперь если у нас есть сущность x и сущность 3, то x+3 вернет сущность оператора суммы с двумя детьми: 3 и x. Так, мы можем строить деревья выражений.

Вызов функции более простой и не такой красивый, как с оператором:

Подвешивание в репе реализовано тут.

Отлично, мы составили дерево выражений.

Подстановка переменной

Здесь все предельно просто. У нас есть Entity — мы проверяем является ли он сам переменной, если да, возвращаем значение, иначе — бежим по детям.

В этом огромном 48-строчном файле реализована столь сложная функция.

Вычисление значения

Собственно то, ради чего все это. Здесь мы по идее должны добавить в Entity какой-то такой метод

Листик без изменений, а для всего остального у нас кастомное вычисление. Опять же, приведу лишь пример:

Если аргумент — число, то произведем численную функцию, иначе — вернем как было.

Number?

Это самая простая единица, число. Над ним можно проводить арифметические операции. По умолчанию оно комплексное. Также у него определены такие операции как Sin, Cos, и некоторые другие.

Если интересно, Number описан тут.

Производная

Численно производную посчитать может кто угодно, и такая функция пишется поистине в одну строку:

Но разумеется нам хочется аналитическую производную. Так как у нас уже есть дерево выражений, мы можем рекурсивно заменить каждый узел в соответствии с правилом дифференциирования. Работать оно должно примерно так:

Вот, к примеру, как реализованна сумма в моем коде:

А вот произведение

А вот сам по себе обход:

Это метод Entity. И как видим, что у листа всего два состояния — либо это переменная, по которой мы дифференциируем, тогда ее производная равна 1, либо это константа (число либо VariableEntity), тогда ее производная 0, либо узел, тогда идет отсылка по имени (InvokeDerive обращается к словарю функций, где и находится нужная (например сумма или синус)).

Заметьте, я здесь не оставляю что-то типа dy/dx и сразу говорю, что производная от переменной не по которой мы дифференциируем равна 0. А вот здесь сделано по-другому.

Все дифференциирование описано в одном файле, а больше и не надо.

Упрощение выражения. Паттерны

Упрощение выражения в общем случае в принципе нетривиально. Ну например, какое выражение проще: или ? Но мы придерживаемся каких-то представлений, и на основе них хотим сделать те правила, которые точно упрощают выражение.

Можно при каждом Eval писать, что если у нас сумма, а дети — произведения, то переберем четыре варианта, и если где-то что-то равно, вынесем множитель… Но так делать конечно же не хочется. Поэтому можно догадаться до системы правил и паттернов. Итак, что мы хотим? Примерно такой синтаксис:

Вот пример дерева, в котором нашлось поддерево (обведено в зеленый), отвечающее паттерну any1 + const1 * any1 (найденное any1 обведено в оранжевый).

Как видим, иногда нам важно, что одна и та же сущность должна повторяться, например чтобы сократить выражение x + a * x нам необходимо, чтобы и там и там был x, ведь x + a * y уже не сокращается. Поэтому нам нужно сделать алгоритм, который не только проверяет, что дерево соответсвует паттерну, но и

1. Проверять, что одинаковые паттерновые Entity соответствуют одинаковым Entity.
2. Записывать, что чему соответствует, чтобы потом подставить.

Точка входа выглядит примерно так:

А в tree.PaternMakeMatch мы рекурсивно наполняем словарь ключами и их значениями. Вот пример списка самих паттерных Entity:

Когда мы будем писать any1 * const1 — func1 и так далее, у каждой ноды будет номер — это и есть ключ. Иначе говоря, при заполнении словаря, ключами выступят как раз эти номера: 100, 101, 200, 201, 400… А при постройке дерева мы будем смотреть на значение, соответствующее ключу, и подставлять его.

Упрощение. Сортировка дерева

В статье, к которой я уже обращался, автор решил сделать просто, и отсортировал практически по хешу дерева. Ему удалось сократить a и -a, b + c + b превратить 2b + c. Но мы, конечно, хотим и чтобы (x + y) + x * y — 3 * x сокращалось, и в целом более сложные штуки.

Паттерны не работают?

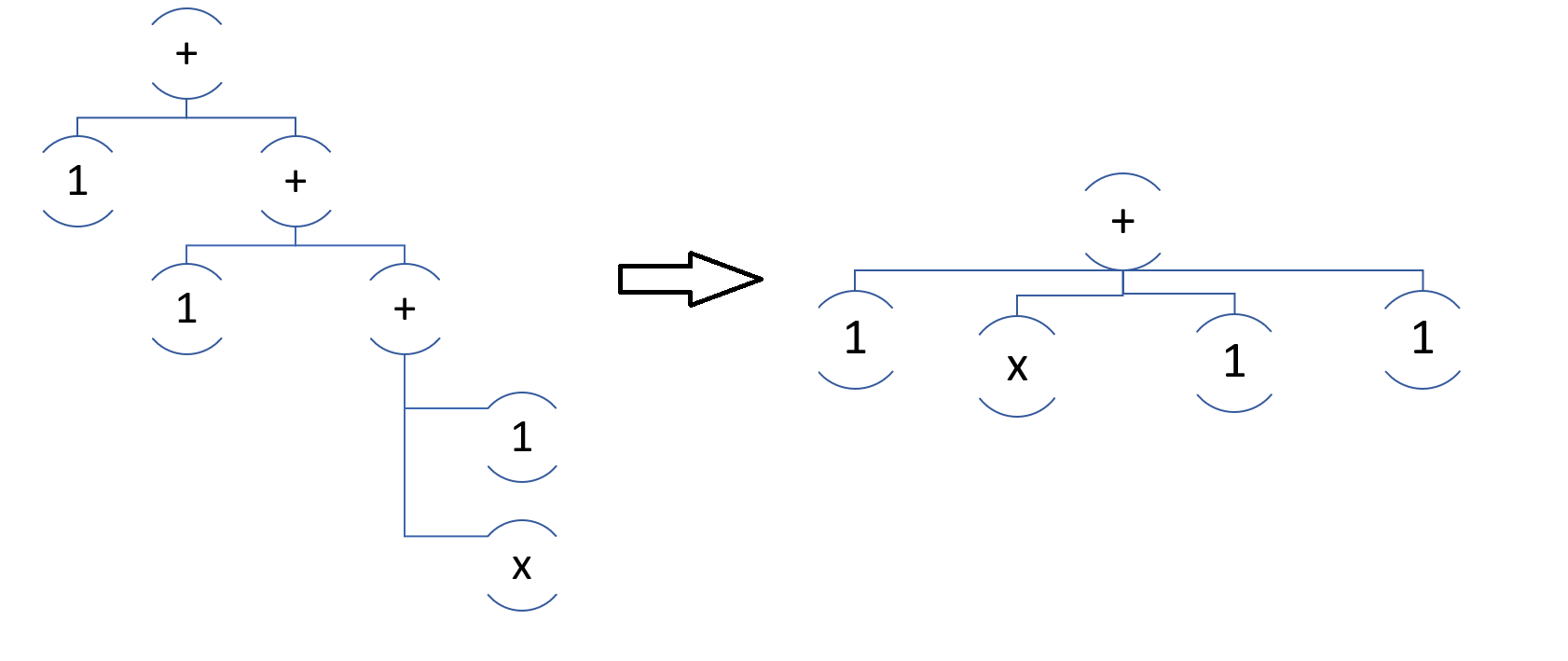
Вообще, то, что мы сделали до этого, паттерны — чудовищно замечательная штука. Она позволит вам сокращать и разность квадратов, и сумму квадрата синуса и косинуса, и другие сложные штуки. Но элементарную пальму, ((((x + 1) + 1) + 1) + 1), она не сократит, ведь здесь главное правило — коммутативность слагаемых. Поэтому первый шаг — вычленить «линейных детей».

«Линейные дети»

Собственно для каждой ноды суммы или разности (и, кстати, произведения/деления) мы хотим получить список слагаемых (множителей).

Это в принципе несложно. Пусть функция LinearChildren(Entity node) возвращает список, тогда мы смотрим на child in node.Children: если child — это не сумма, то result.Add(child), иначе — result.AddRange(LinearChildren(child)).

Не самым красивым образом реализовано тут.

Группировка детей

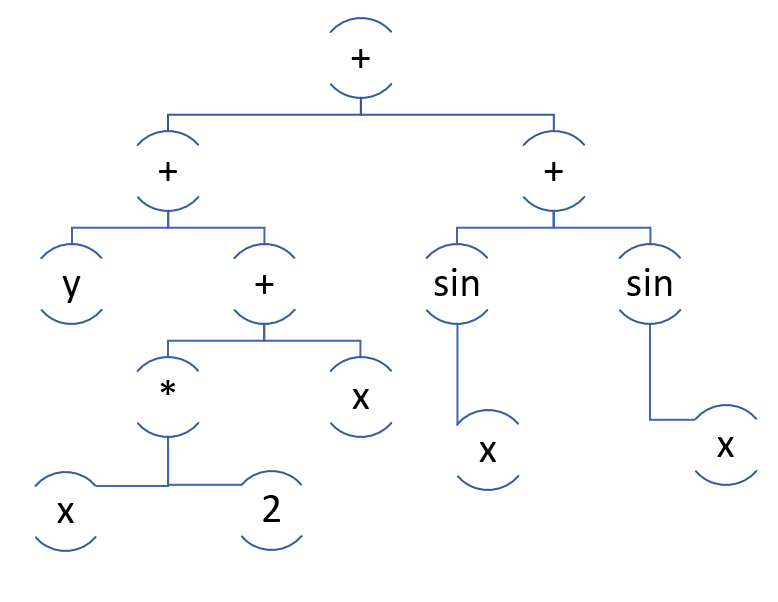
Итак, у нас есть список детей, но что дальше? Допустим, у нас есть sin(x) + x + y + sin(x) + 2 * x. Очевидно, что наш алгоритм получит пять слагаемых. Далее мы хотим сгруппировать по похожести, например, x похож на 2 * x больше, чем на sin(x).

Вот хорошая группировка:

Так как в ней паттерны дальше справятся с преобразованием 2*x + x в 3*x.

То есть мы сначала группируем по некоторому хешу, а затем делаем MultiHang — преобразование n-арного суммирования в бираное.

Хеш узла

С одной стороны, и следует поместить в одну группу. С другой стороны, при наличии помещать в одну группу с бессмысленно.

Поэтому мы реализовываем многоуровневую сортировку. Сначала мы делаем вид, что — одно и то же. Посортировали, успокоились. Потом делаем вид, что можно помещать только с другими . И вот уже наши и наконец объединились. Реализовано достаточно просто:

Как видим, функция по-любому влияет на сортировку (разумеется, ведь с вообще никак в общем случае не связана). Как и переменная, с ну никак не получится смешать. А вот константы и операторы учитываются не на всех уровнях. В таком порядке идет сам процесс упрощения

«Компиляция» функций

В кавычках — так как не в сам IL код, а лишь в очень быстрый набор инструкций. Но зато очень просто.

Проблема Substitute

Чтобы посчитать значение функции, нам достаточно вызвать подстановку переменной и eval, например

Но это работает медленно, около 1.5 микросекунды на синус.

Инструкции

Чтобы ускорить вычисление, мы делаем вычисление функции на стеке, а именно:

1) Придумываем класс FastExpression, у которого будет список инструкций

2) При компиляции инструкции складываются в стек в обратном порядке, то есть если есть функция x * x + sin(x) + 3, то инструкции будут примерно такими:

Далее при вызове мы прогоняем эти инструкции и возвращаем Number.

Пример выполнения инструкции суммы:

Вызов синуса сократился с 1500нс до 60нс (системный Complex.Sin работает за 30нс).
В репе реализовано тут.

Фух, вроде бы пока все. Хотя рассказать еще есть о чем, но мне кажется объем для одной статьи достаточный. Интересно ли кому-нибудь продолжение? А именно: парсинг из строки, форматирование в латех, определенный интеграл, и прочие плюшки.

Ссылка на репозиторий со всем кодом, а также тестами и самплами.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.