Контрольная сумма crc32 linux

Проверка контрольных сумм файлов в Linux

Очень часто при загрузке файлов с Интернет-ресурсов можно встретить прилагаемую информацию о контрольных суммах этих файлов. Многие пользователи просто не обращают на это внимания, скачивают файл и используют его «как есть». Однако контрольные суммы к соответствующим загружаемым файлам прилагаются не просто так. Это напрямую связано с корректной работой программ (если это исполняемые файлы), а также с безопасностью. В данной статье будет более подробно изложено, почему так важно пользоваться контрольными суммами, а также рассмотрены способы проверки файлов в Linux.

Зачем нужно выполнять проверку файлов?

Контрольные суммы загружаемых файлов позволяют определить, что файл — точная копия того, что хранится на сервере, с которого он был загружен. Структура файлов, особенно таких больших и сложных, как например, ISO-образы может быть повреждена в процессе загрузки (могут удаляться TCP-пакеты из-за некачественной связи и т. п.) и таким образом, загруженные файлы нельзя будет полноценно использовать. Например, не откроется или не распакуется архив.

Есть и другой важный аспект в использовании контрольный сумм — это безопасность. Удалённый сервер, с которого происходит загрузка файлов может быть взломан, а сами загружаемые файлы на нём — изменены. Изменения могут быть не самыми безобидными, как можно понимать. Проверка контрольных сумм может выявить «подлог» ещё до того как загруженный файл будет обработан пользователем, конечно, если эта проверка будет своевременной.

Конечно же злоумышленник, может подменить и сами контрольные суммы, соответственно «испорченным» файлам. Но «лишняя» посторонняя активность на сервере легко может быть замечена и, соответственно, пресечена. Да и для того, чтобы злоумышленнику отредактировать соответствующие публикации на сайтах, предоставляющих загрузки, ему нужно, возможно, преодолевать защиту ещё и самих сайтов, а значит, неоправданно рисковать. Поэтому в подавляющем большинстве случаев такие действия ограничиваются быстрой подменой оригинальных файлов на «контрафактные». Но независимо от того, каким образом были модифицированы загружаемые файлы, всегда следует их проверять, когда предоставляются их контрольные суммы.

Каким образом это работает?

Создание контрольных сумм файлов называется хешированием. Сама же контрольная сумма — это некоторая строка определённой длины, состоящая из последовательности букв и цифр. Нужно заметить, хеширование никоим образом не зашифровывает файл, а контрольная сумма ничего не расшифровывает. Контрольная сумма называется суммой потому, что это результат однонаправленного криптографического «суммирования» — специального алгоритма. А контрольной она называется потому, что её значение (как и длина контрольной строки — обычно 32 символа) будет всегда одним и тем же, если файл никак не изменялся, независимо от того, сколько раз и при каких условиях вычисляется его контрольная сумма. Но стоит над файлом произвести даже самые незначительные изменения (например, вставить один лишний пробел в текстовом файле), как значение контрольной суммы изменится. Таким образом, значение контрольной суммы меняется, если хотя бы один бит файла изменился.

Для создания и проверки контрольный сумм существует два основных метода: MD5 и SHA. Первый считается устаревшим, поскольку для задач шифрования может быть относительно нетрудно взломан. Однако, на работу с контрольными суммами файлов это никак не влияет. Главным же плюсом MD5 является его скорость — она быстрее, чем у SHA, да и вообще других методов шифрования.

Но нельзя не упомянуть также и о том, что в настоящее время всё-таки популярность SHA быстро растёт. В большинстве случаев именно его контрольные суммы публикуются для выкладываемых для загрузки файлов.

SHA имеет несколько версий. Обычно, при публикации это указывается, например: SHA1, SHA2. Это подсказывает пользователю, каким именно инструментом, реализующим одну из версий SHA нужно воспользоваться при проверке. Если же контрольная сумма указана без номера, то это SHA1. Вообще, для проверки целостности файлов оба метода одинаково хороши, выбор зависит от того, контрольная сумма какого метода опубликована для загружаемых файлов.

Что для этого нужно?

Для проверки файлов в системах Linux используются утилиты, которые практически всегда предустановлены в системе. Для этого достаточно вызвать соответствующие команды в командной оболочке.

В качестве проверяемых файлов используются любые файлы, для которых публикуются исходные контрольные суммы, например образы дистрибутивов Ubuntu или Rosa Linux. Далее в примерах будет использоваться образ ROSA.FRESH.PLASMA5.R11.x86_64.uefi.iso.

Как проверить файл в Linux?

Для начала скачаем сам файл, т. е. ISO-образ. На странице загрузки в списке рядом со ссылкой на образ есть также и ссылки на текстовые файлы

содержащие значения соответствующих (как видно из расширений этих файлов) контрольных сумм. Их тоже нужно скачать.

Итак, загрузка образа, используя утилиту wget:

Загрузка файла с контрольной суммой SHA1:

Просмотр содержащегося в файле ROSA.FRESH.PLASMA5.R11.x86_64.uefi.iso.sha1sum значения контрольной суммы SHA1 с помощью команды cat:

Как можно видеть, представлены контрольная сумма и имя образа, для которого она была вычислена. Теперь можно, собственно, проверить сам образ, используя для этого команду sha1sum;

Зрительно сопоставив значения контрольных сумм из вывода команды sha1sum и из содержимого файла PLASMA5.R11.x86_64.uefi.iso.sha1sum, можно убедиться, что они полностью совпадают. Таким образом, загруженный образ идентичен тому, что находится на сервере и его можно смело использовать.

Следует отметить, что версии SHA отличаются количеством следующих друг за другом запусков SHA – 256, 384 и 512. Для всех этих версий существуют соответствующие команды: sha256sum, sha384sum и sha512sum. Аналогичным образом можно использовать и команду md5sum для проверки контрольных сумм MD5.

Заключение

Итак, были рассмотрены самые распространённые способы проверки файлов. Как можно видеть, это совсем не сложно и выполняется стандартными средствами в любой системе Linux буквально одной командой.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

Проверка контрольной суммы Linux

Контрольная сумма — это цифра или строка, которая вычисляется путем суммирования всех цифр нужных данных. Ее можно использовать в дальнейшем для обнаружения ошибок в проверяемых данных при хранении или передаче. Тогда контрольная сумма пересчитывается еще раз и полученное значение сверяется с предыдущим.

В этой небольшой статье мы рассмотрим что такое контрольная сумма Linux, а также как выполнять проверку целостности файлов с помощью контрольных сумм md5.

Что такое MD5?

Контрольные суммы Linux с вычисляемые по алгоритму MD5 (Message Digest 5) могут быть использованы для проверки целостности строк или файлов. MD5 сумма — это 128 битная строка, которая состоит из букв и цифр. Суть алгоритма MD5 в том, что для конкретного файла или строки будет генерироваться 128 битный хэш, и он будет одинаковым на всех машинах, если файлы идентичны. Трудно найти два разных файла, которые бы выдали одинаковые хэши.

В Linux для подсчета контрольных сумм по алгоритму md5 используется утилита md5sum. Вы можете применять ее для проверки целостности загруженных из интернета iso образов или других файлов.

Эта утилита позволяет не только подсчитывать контрольные суммы linux, но и проверять соответствие. Она поставляется в качестве стандартной утилиты из набора GNU, поэтому вам не нужно ничего устанавливать.

Проверка контрольных сумм в Linux

Синтаксис команды md5sum очень прост:

$ md5sum опции файл

Опций всего несколько и, учитывая задачи утилиты, их вполне хватает:

• -c — выполнить проверку по файлу контрольных сумм;
• -b — работать в двоичном формате;
• -t — работать в текстовом формате;
• -w — выводить предупреждения о неверно отформатированном файле сумм;
• —quiet — не выводить сообщения об успешных проверках.

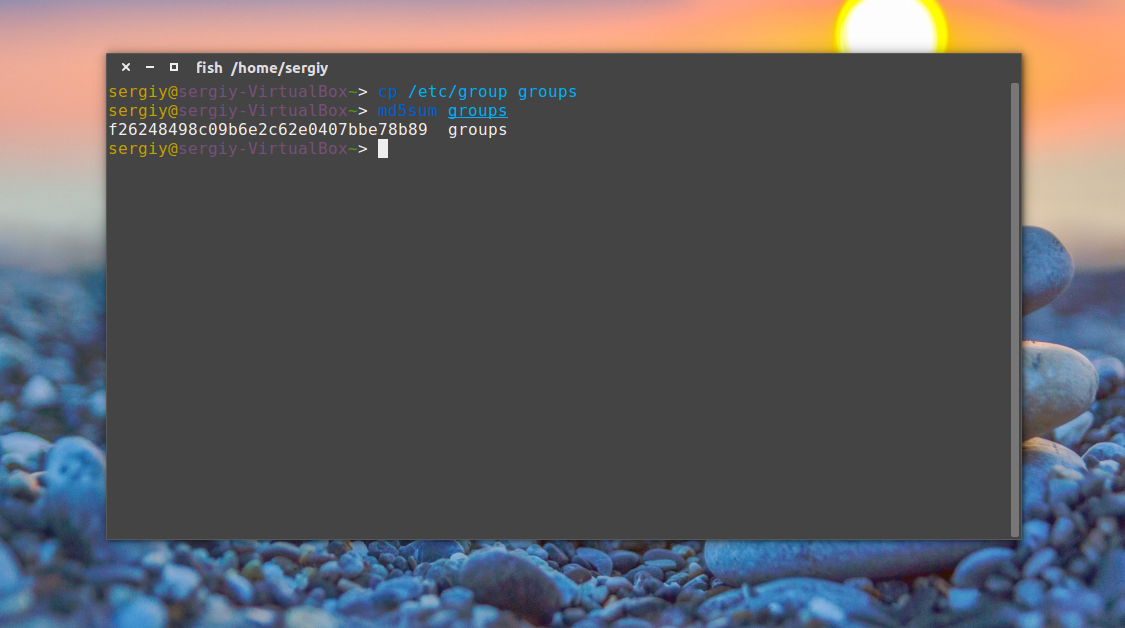
Сначала скопируйте файл /etc/group в домашнюю папку чтобы на нем немного поэкспериментировать:

cp /etc/group groups

Например, давайте подсчитаем контрольную сумму для файла /etc/group:

Или вы можете сохранить сразу эту сумму в файл для последующей проверки:

md5sum groups > groups.md5

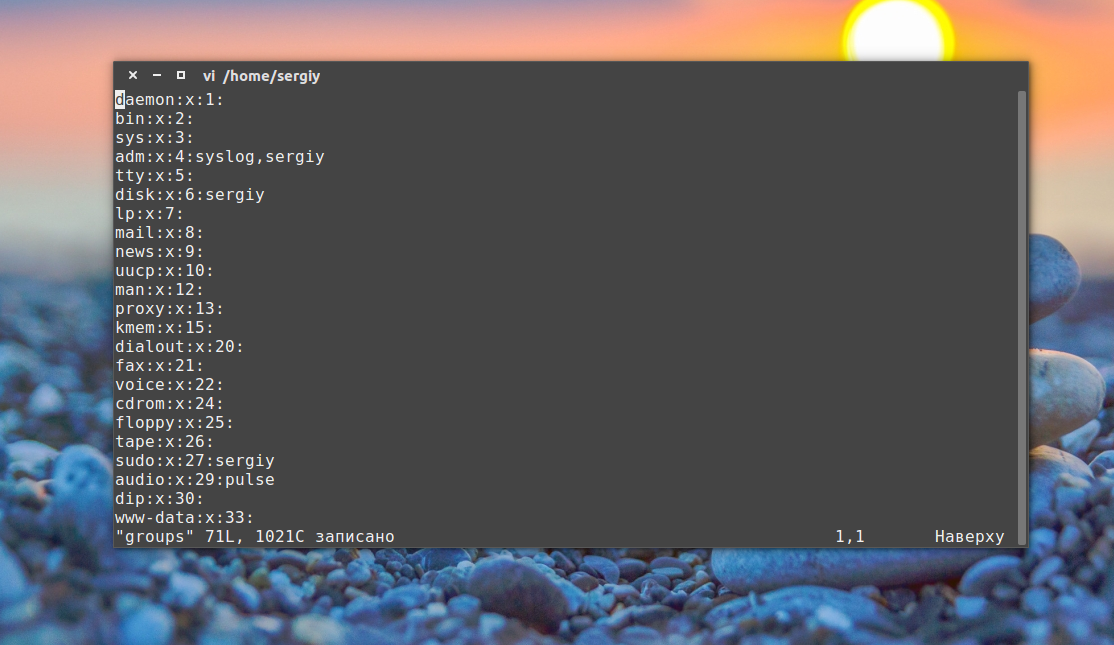
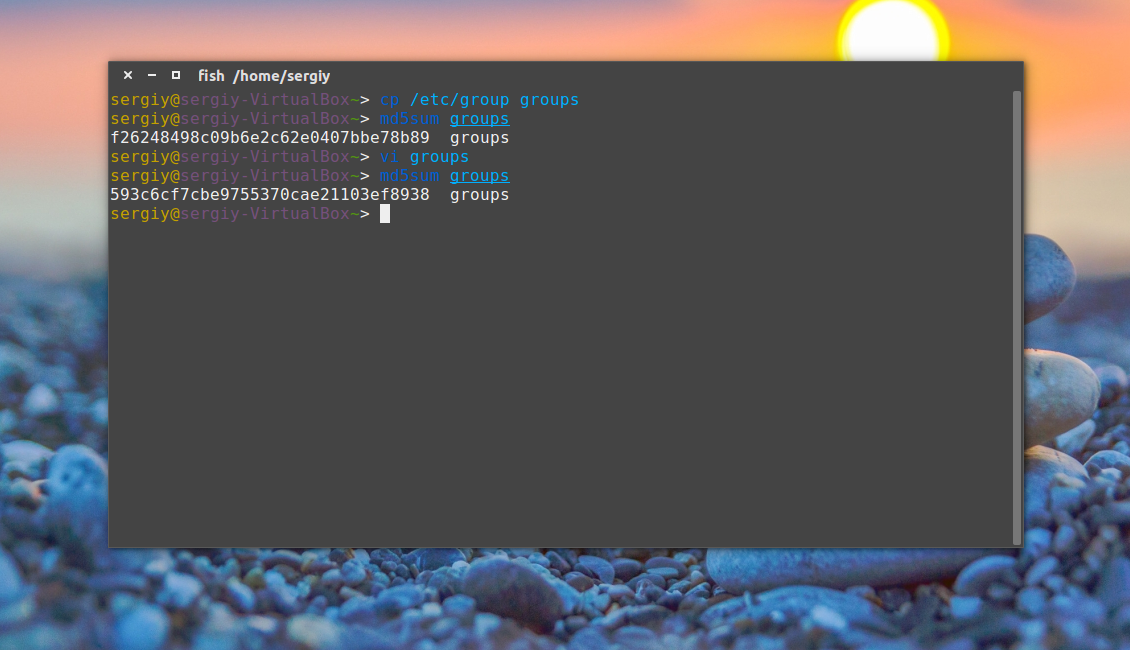
Затем каким-либо образом измените этот файл, например, удалите первую строчку и снова подсчитайте контрольные суммы:

Как видите, теперь значение отличается, а это значит, что содержимое файла тоже изменилось. Дальше верните обратно первую строчку root:x:0: и скопируйте этот файл в groups_list и

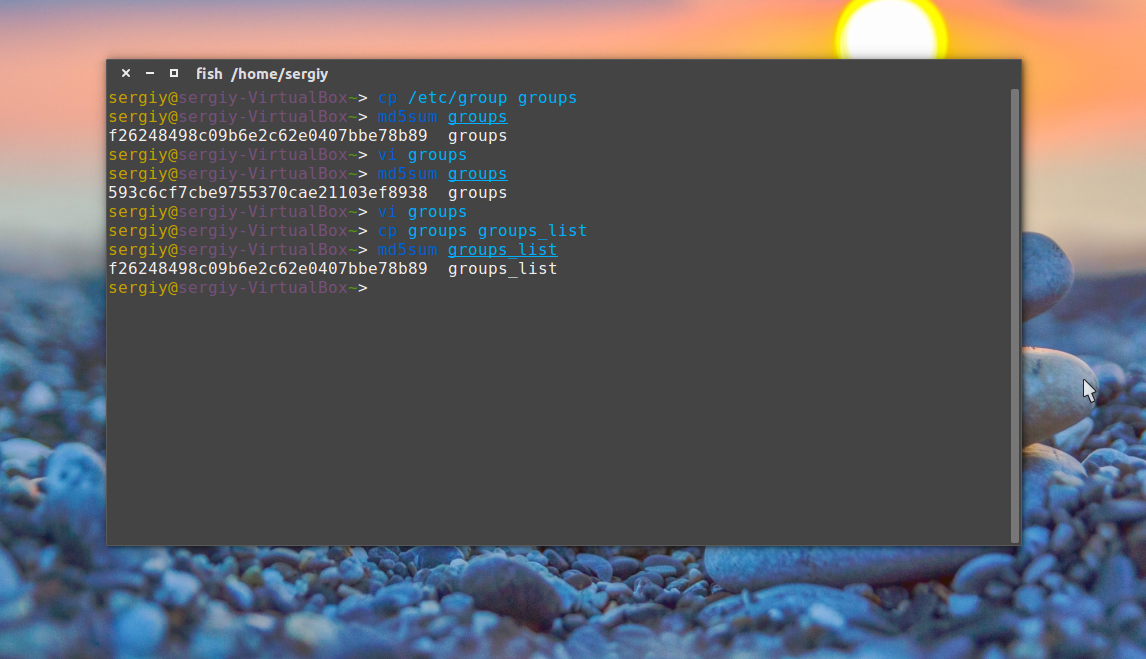
cp groups groups_list

Затем опять должна быть выполнена проверка контрольной суммы linux:

Сумма соответствует первому варианту, даже несмотря на то, что файл был переименован. Обратите внимание, что md5sum работает только с содержимым файлов, ее не интересует ни его имя, ни его атрибуты. Вы можете убедиться, что оба файла имеют одинаковые суммы:

md5sum groups groups_list

Вы можете перенаправить вывод этой команды в файл, чтобы потом иметь возможность проверить контрольные суммы:

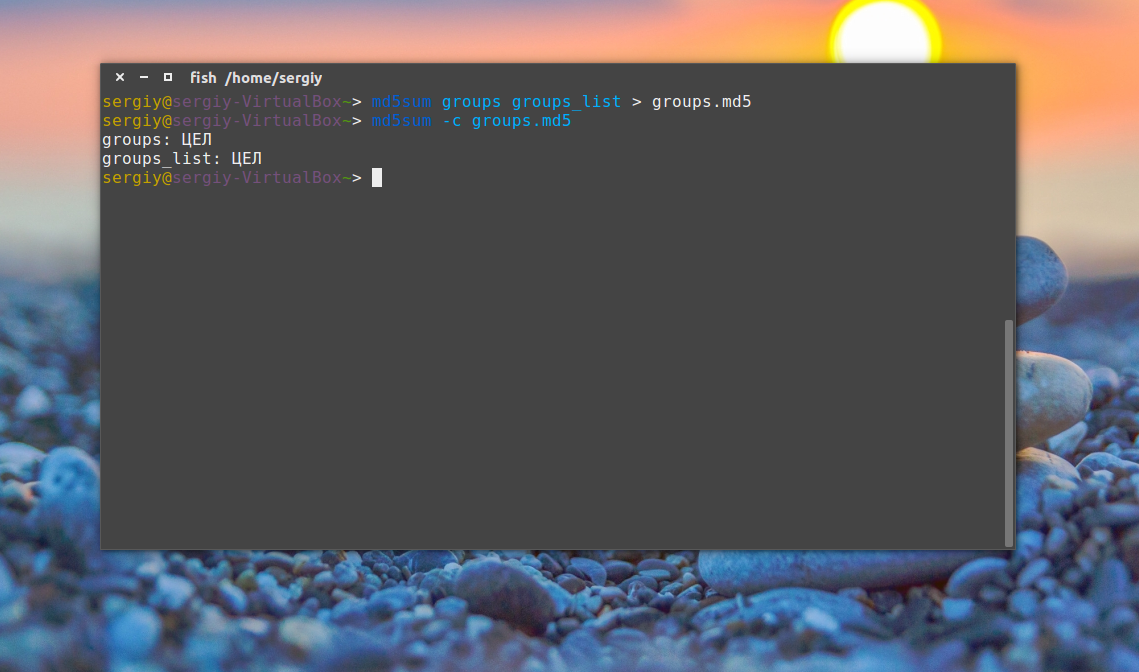
md5sum groups groups_list > groups.md5

Чтобы проверить, не были ли файлы изменены с момента создания контрольной суммы используйте опцию -c или —check. Если все хорошо, то около каждого имени файла появится слово OK или ЦЕЛ:

md5sum -c groups.md5

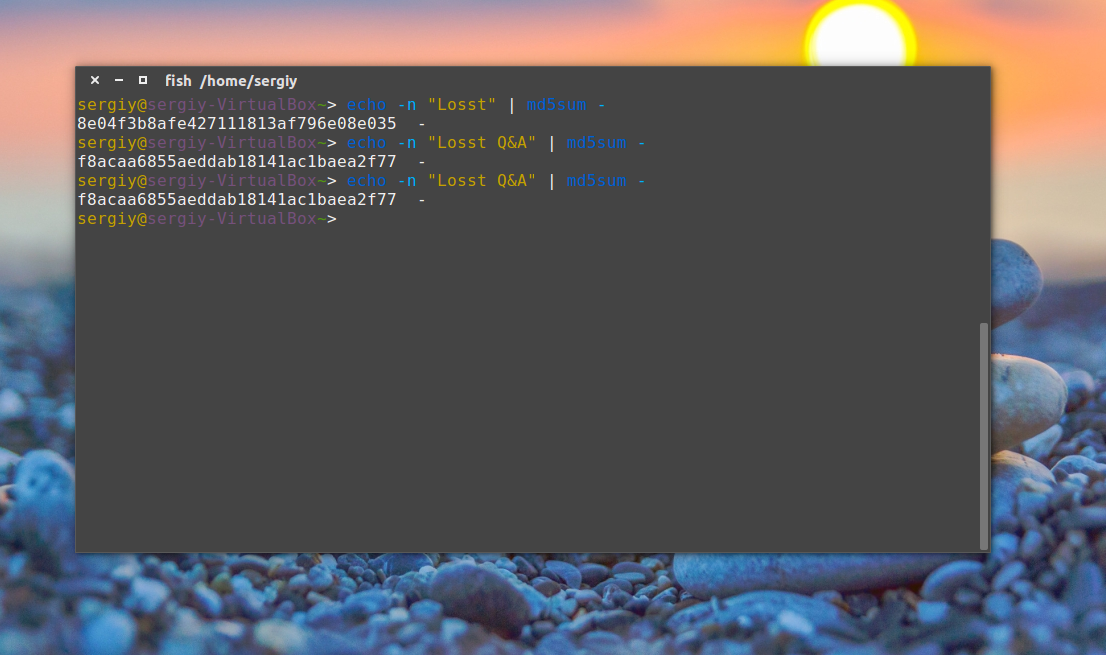
Но теперь вы не можете переименовывать файлы, потому что при проверке утилита будет пытаться открыть их по имени и, естественно, вы получите ошибку. Точно так же все работает для строк:

echo -n «Losst» | md5sum —
$ echo -n «Losst Q&A» | md5sum —

Выводы

Из этой статьи вы узнали как выполняется получение и проверка контрольной суммы linux для файлов и строк. Хотя в алгоритме MD5 были обнаружены уязвимости, он все еще остается полезным, особенно если вы доверяете инструменту, который будет создавать хэши.

Проверка целостности файлов Linux — это очень важный аспект использования системы. Контрольная сумма файла Linux используется не только вручную при проверке загруженных файлов, но и во множестве системных программ, например, в менеджере пакетов. Если у вас остались вопросы, спрашивайте в комментариях!

На завершение небольшое видео по теме:

Источник

Простой расчет контрольной суммы

При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.

Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.

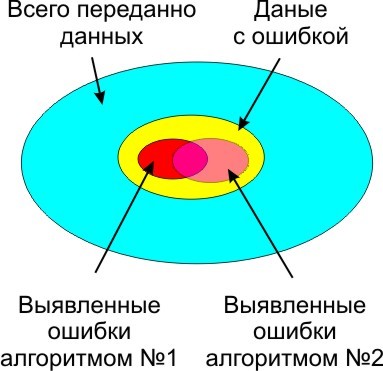
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.

Причина помех на физическом уровне, при передаче данных.

Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.

Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.

Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.

Бит четности (1-битная контрольная сумма)

На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:

Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.

8-битная контрольная сумма

Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично

Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:

1. Блок данных 8 байт.
2. Заполненность псевдослучайными данными Random($FF+1)
3. Случайным образом меняем 1 бит в блоке данных операцией XOR со специально подготовленным байтом, у которого один единичный бит на случайной позиции.
4. Повторяем предыдущий пункт 10 раз, при этом может получится от 0 до 10 сбойных бит (2 ошибки могут накладываться друг на друга восстанавливая данные), вариант с 0 сбойных бит игнорируем в дальнейшем как бесполезный для нас.

Передаем виртуальную телеграмму N раз. Идеальная контрольная сумма выявит ошибку по количеству доступной ей информации о сообщении, больше информации, выше вероятность выявления сбойной телеграммы. Вероятность пропустить ошибку, для 1 бита контрольной суммы:

.

,

на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:

Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).

Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.

Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.

Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.

Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:

Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:

Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов

• Промежуточная CRC для первого действия 16-битная (после вычислений обрезается до 8 бит) и в дальнейшем работаем как с 8-битной, если у нас 8-битный микроконтроллер это ускорит обработку данных.
• Возвращаем старшие биты и перемешиваем с младшими.

Проверяем:

Результат 91% от теоретического предела. Вполне годится для применения.

Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.

На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.

Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.

Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:

Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.

Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).

Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:

Результат 100.6% от теоретического предела.

Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:

Результат 86% от теоретического предела.

В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).

Небольшое улучшение в некоторых случаях дает так же:

• Двойной проход по обрабатываемым данным. Но ценой усложнения алгоритма (внешний цикл нужно указать), ценой удвоения времени обработки данных.
• Обработка дополнительного, виртуального байта в конце обрабатываемых данных, усложнения алгоритма и времени работы алгоритма практически нет.
• Использование переменной для хранения контрольной суммы большей по разрядности, чем итоговая контрольная сумма и перемешивание младших бит со старшими.

Результат работы рассмотренных алгоритмов, от простых и слабых, к сложным и качественным:

16-битная контрольная сумма

Далее, предположим что нам мало 8 бит для формирования контрольной суммы.

Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.

Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.

Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.

Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.

Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.

32-битная контрольная сумма

Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения

За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:

Результат, из 10 млн. итераций ошибка обнаружена 3 раза

Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.

Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.

Вариант без умножения:

Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.

64-битная контрольная сумма

Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:

Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 🙂

Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.

Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.

Комментарии

В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.

Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.

Мой проект по исследованию CRC на гитхаб.

Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.

Источник