Linux перевод систем счисления

12.8. Команды выполнения математических операций

Разложение целого числа на простые множители.

Bash не в состоянии выполнять действия над числами с плавающей запятой и не содержит многих важных математических функций. К счастью существует bc.

Универсальная, выполняющая вычисления с произвольной точностью, утилита bc обладает некоторыми возможностями, характерными для языков программирования.

Синтаксис bc немного напоминает язык C.

Поскольку это утилита UNIX, то она может достаточно широко использоваться в сценариях на языке командной оболочки, в том числе и в конвейерной обработке данных.

Ниже приводится простой шаблон работы с утилитой bc в сценарии. Здесь используется прием подстановки команд.

Пример 12-32. Ежемесячные выплаты по займу

Пример 12-33. Перевод чисел из одной системы счисления в другую

Один из вариантов вызова bc — использование вложенного документа, внедряемого в блок с подстановкой команд. Это особенно актуально, когда сценарий должен передать bc значительный по объему список команд и аргументов.

Пример 12-34. Пример взаимодействия bc со «встроенным документом»

Пример 12-35. Вычисление числа «пи»

Утилита dc ( desk calculator) — это калькулятор, использующий «Обратную Польскую Нотацию», и ориентированный на работу со стеком.

Многие стараются избегать испоьзования dc, из-за непривычной формы записи операндов и операций. Однако, dc имеет и своих сторонников.

Пример 12-36. Преобразование чисел из десятичной в шестнадцатиричную систему счисления

Изучение страниц info dc позволит детальнее разобраться с утилитой. Однако, отряд «гуру», которые могут похвастать своим знанием этой мощной, но весьма запутанной утилиты, весьма немногочислен.

Пример 12-37. Разложение числа на простые множители

Еще один способ выполнения математических операций, над числами с плавающей запятой, состоит в создании сценария-обертки, использующего математические функции awk.

Пример 12-38. Расчет гипотенузы прямоугольного треугольника

Источник

GNU bc — калькулятор командной строки для Linux

Оригинал: What is a good command-line calculator on Linux
Автор: Dan Nanni
Дата публикации: 21 октября 2014 года
Перевод: А. Кривошей
Дата перевода: октябрь 2015 г.

Любой современный дистрибутив Linux включает графический калькулятор. С другой стороны, если вашим обычным рабочим окружением является терминал, то вы скорее будете искать себе калькулятор, который бы работал в командной строке. В этой категории программ, по моему мнению, единоличным лидером является GNU bc (сокращение от «basic calculator»). Это очень мощная и полезная утилита.

Еще до наступления эры GNU, bc исторически был известным языком для вычислений, первая реализация которого относится к старым добрым временам Unix 70-х годов. Изначально bc был больше известен в качестве языка программирования с синтаксисом, похожим на C. Со временем оригинальный bc эволюционировал в POSIX bc, а затем и в GNU bc.

Возможности GNU bc

Сегодняшний GNU bc является результатом многочисленных усовершенствований предыдущих реализаций, и сегодня он представляет собой стандарт для всех главных дистрибутивов GNU/Linux. bc поддерживает стандартные арифметические операции с числами произвольной точности и различных систем счисления (двоичные, десятеричные, шестнадцатеричные).

Если вы знакомы с языком C, вы увидите, что в bc используются те же или похожие математические операторы. Среди поддерживаемых операций арифметические (+,-,*,/,%,++,—), сравнения ( ,==,!=, =), логические (!,&&,||), побитовые (&,|,^,

, >), составного присваивания (+=,-=,*=,/=,%=,&=,|=,^=,&&=,||=, >=). bc имеет много полезных встроенных функций, таких как извлечение квадратного корня, тригонометрические и обратные тригонометрические функции, логарифмы, экспонента и так далее.

Использование GNU bc

Возможности GNU bc как калькулятора командной строки практически неограничены. В этом руководстве я собираюсь описать самые популярные функции bc. Получить полную информацию о возможностях программы можно из официальной документации.

За исключением случая запуска ранее написанного скрипта, обычно bc используется в интерактивном режиме, где каждая строка, содержащая выражение или оператор, интерпретируется и выполняется на лету. Чтобы перейти в интерактивную сессию bc, введите приведенную ниже команду. Для выхода из сессии введите «quit» и нажмите Enter.

Во всех приведенных в данном руководстве примерах подразумевается, что они вводятся внутри сессии bc.

Типы выражений

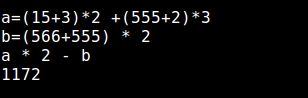
Для расчета арифметического выражения просто введите выражение и нажмите Enter. Если хотите, можете сохранить промежуточный вариант в переменной, чтобы затем использовать его в других выражениях.

В пределах одной сессии bc сохраняет всю историю введенных строк. Для возврата к предыдущим выражениям используется курсорная клавиша со стрелкой вверх. Если вы хотите ограничить число строк, сохраняемых в истории, присвойте нужное вам число переменной по имени history. По умолчанию ее значение -1, что соответствует «unlimited».

Переключение между системами счисления ввода/вывода

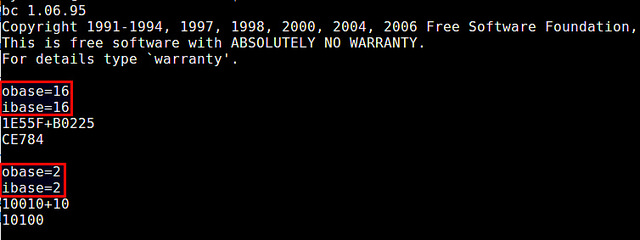
Часто может потребоваться вводить числа и выводить на экран результаты в двоичном или шестнадцатеричном формате. Для этого bc позволяет определить систему счисления для ввода и вывода. Они хранятся в переменных ibase и obase соответственно. По умолчанию значение этих специальных переменных равно 10, а диапазон допустимых значений от 2 до 16 (или значения переменной окружения BC_BASE_MAX в случае obase). Все, что вам нужно для смены системы счисления — изменить значения ibase и obase. Например, ниже пример суммирования двух шестнадцатеричных/двоичных чисел:

Обратите внимание, что я задал сначала obase=16, затем ibase=16, а не наоборот. Если бы задал сначала ibase=16, то выражение obase=16 интерпретировалось бы уже в шестнадцатеричном формате (то есть мы присваивали бы obase значение 22 в десятеричной форме).

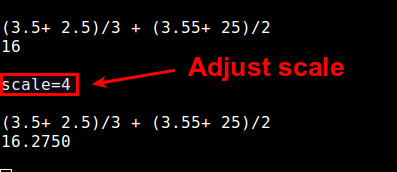
Точность

В bc точность чисел хранится в специальной переменной под названием scale (количество десятичных цифр после точки). По умолчанию ее значение равно 0, что соответствует хранению всех цифр результата. Вы можете изменить точность, присвоив перменной scale соответствующее значение.

Использование встроенных функций

Помимо простых арифметических операций GNU bc предлагает большой набор продвинутых математических функций, как встроенных, так и находящихся во внешней математической библиотеке. Для использования этих функций запустите bc с опцией «-l».
Ниже проиллюстрированы некоторые из этих встроенных функций.

Квадратный корень из N:

Синус от X (X в радианах):

Косинус от X (X в радианах):

Арктангенс от X (возвращаемое значение в радианах):

Натуральный логарифм от X:

Экспонента от X:

Другие возможности языка

GNU bc поддерживает простые операторы (например присваивание значения переменной, break, return), составные операторы (if, while, for loop), и функции, определенные пользователем. Я не буду детально описывать эти возможности, но вы легко можете научиться пользоваться ними из официального руководства. Ниже пример определения очень простой функции:

Неинтерактивное использование GNU bc

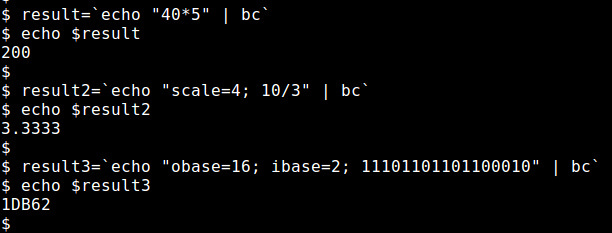
До сих пор мы использовали bc в интерактивном режиме. Однако достаточно часто он используется неинтерактивно, в скриптах оболочки. В этом случае вы можете направить ввод на bc с помощью команды echo, например:

В завершение можно сказать, что GNU bc — это очень мощный гибкий калькулятор командной строки, который соответствует самым высоким требованиям. Предустановленный во всех современных дистрибутивах Linux, bc может значительно упростить ваши задачи, не выходя из терминала.

Источник

Небольшие заметки о Linux

Thursday, September 10, 2015

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления — самым старшим разрядом в новой записи числа.

Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.

Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).

• в двоичном коде:;
• в восьмеричном коде;
• в шестнадцатеричном коде —.

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.

Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы

Таблица 11.2. Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков

Двоичная группа	Шестнадцатеричный знак	Десятичный эквивалент	Двоичная группа	Восьмеричный знак
0000	0	0	000	0
0001	1	1	001	1
0010	2	2	010	2
0011	3	3	011	3
0100	4	4	100	4
0101	5	5	101	5
0110	6	6	110	6
0111	7	7	111	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

• перевод в шестнадцатеричную систему:

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже — в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной (восьмеричной) системы счисления в двоичную по следующему правилу.

Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).

Источник
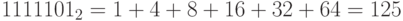