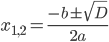Решение квадратного уравнения windows forms

Уроки Windows Forms C++/C#

Решение квадратного уравнения в Windovs Forms MVS C++

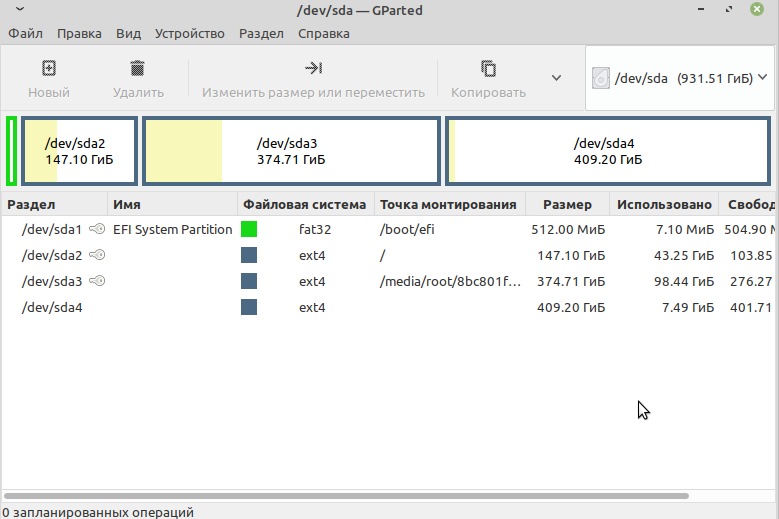
В этом уроке мы с вами напишем программу для решения квадратного уравнения. Причём она сможет решать уравнения с отрицательным дескрименантом и находить комплексные корни. Пользователю нужно будет лишь ввести коэффициенты, а программа в текстовом виде выдаст результат. Как вы уже поняли — это будет вполне полноценная и прикладная программа, которая может оказаться вполне актуальна для школьников средних классов и для начинающих программистов. В разделе, посвящённом урокам C++» описывалось “решение квадратного уравнения”, по этому нам нужно теперь вставить это решение в новое приложение, нужным образом оформив его. И так, приступим. Для этого нам понадобятся: 3 «textBox», 5 «label» и кнопка “button”. Как изменять шрифт «label», вы можете узнать из этого урока, по этому оформить должным образом форму программы для вас не будет сложностью. Вот как она должна выглядеть:

После этого, в коде ещё раз написан текст для каждого «lable». Из предыдущего урока вы могли узнать, как ограничить возможность вводить любые знаки. В данном проекте это так же будет использоваться, что бы пользователь мог вводить только цифры. После того как программа запуститься пользователю нужно будет ввести коэффициенты, после вычислений программа покажет корни, даже, если они будут комплексные, так же будет показан дискриминант, но это всё конечно же нужно сначала описать в коде. Для «textBox»ов выбираем событие «KeyPress». Что бы размер формы был фиксирован – выберите свойство «FormBorderStyles»->»Fixed3D». Ну а теперь собственно сам код программы:

#pragma endregion String^ TorZ; private: System::Void Form1_Load(System::Object^ sender, System::EventArgs^ e) < this->Text = «Решение Квадратного Уравнения»; button1->Text = «Вычислить»; label1->Text = «X»; label2->Text = «2»; label3->Text = «+»; label4->Text = «X»; label5->Text = «= 0»; label6->Text = «Введите коэвициенты»; // a b c label7->Text = «»; label8->Text = «»; TorZ = Globalization::NumberFormatInfo::CurrentInfo->NumberDecimalSeparator; > private: System::Void textBox1_KeyPress(System::Object^ sender, System::Windows::Forms::KeyPressEventArgs^ e) < bool TZFound = false; if (Char::IsDigit(e->KeyChar) == true) return; if (e->KeyChar == (char)Keys::Back) return; if (textBox1->Text->IndexOf(TorZ) != -1) TZFound = true; if (TZFound == true) < e->Handled = true; return; > if (e->KeyChar.ToString() == TorZ) return; e->Handled = true; > private: System::Void textBox2_KeyPress(System::Object^ sender, System::Windows::Forms::KeyPressEventArgs^ e) < bool TZFound = false; // Разделительный знак найден if (Char::IsDigit(e->KeyChar) == true) return; if (e->KeyChar == (char)Keys::Back) return; if (textBox2->Text->IndexOf(TorZ) != -1) TZFound = true; if (TZFound == true) < e->Handled = true; return; > if (e->KeyChar.ToString() == TorZ) return; e->Handled = true; > private: System::Void textBox3_KeyPress(System::Object^ sender, System::Windows::Forms::KeyPressEventArgs^ e) < bool TZFound = false; // Разделительный знак найден if (Char::IsDigit(e->KeyChar) == true) return; if (e->KeyChar == (char)Keys::Back) return; if (textBox3->Text->IndexOf(TorZ) != -1) TZFound = true; if (TZFound == true) < e->Handled = true; return; > if (e->KeyChar.ToString() == TorZ) return; e->Handled = true; > private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) < Single a, b, c; Single A = Single::TryParse(textBox1->Text, System::Globalization::NumberStyles::Number, System::Globalization::NumberFormatInfo::CurrentInfo, a); Single B = Single::TryParse(textBox2->Text, System::Globalization::NumberStyles::Number, System::Globalization::NumberFormatInfo::CurrentInfo, b); Single C = Single::TryParse(textBox3->Text, System::Globalization::NumberStyles::Number, System::Globalization::NumberFormatInfo::CurrentInfo, c); float y, z, f, m, k; float D = 0; if (a==0) < MessageBox::Show("Если а = 0 - нет решений!"); >D=b*b-4*a*c; if (D>=0) < y=(-b+sqrt(D))/(2*a); z=(-b-sqrt(D))/(2*a); label7->Text = String::Format(«Корни: x1 = <0:f3>и x2 = <1:f3>«, y, z); label8->Text = String::Format(«При D = <0:f3>«, D); > else< f = -1*D; k = (sqrt(f))/(2*a); m =(-b)/(2*a); label7->Text = String::Format(«Корни: x1 = <0:f1>+ <1:f1>* i и x2 = <0:f1>— <1:f1>* i», m, k); label8->Text = String::Format(«При D = <0:f3>«, D); > > >; >

Результат: Следующий урок >>

Квадратное уравнение

Квадратное уравнение ax 2 + bx + c = 0 на C++ лучше всего решать с помощью формулы, содержащей дискриминант:

Разберем пример кода такой программы:

Данная программа учитывает все исходы при решении подобного уравнения.

Похожие записи:

Квадратное уравнение: 8 комментариев

Добрый день! А как быть со случаями, когда а == 0; b == 0 && c > 0; b == 0 && C !=0 и т.д.?

При a == 0 уравнение перестает называться квадратным. Проблемы также возникают, когда, например, пользователь ввел букву вместо числа. Такие случаи называются аномалиями.
Все аномалии рассмотреть нельзя. Если требуется, то можно, например, рассмотреть аномалию a == 0, добавив после 11-й строки:
if (a == 0)
<
cout

«Все аномалии рассмотреть нельзя.»
Сложно с Вами согласиться. Не такая уж это и нетривиальная задача для программиста — решить уравнение ax2 + bx + c = 0 на C++, учтя все возможные варианты а, b, c, в том числе и когда уравнение перестает быть квадратным и другие.
В противном случае код получается не универсальный, а только для некоторых случаев, когда переменные Вас «устраивают».
Согласитесь — это не решение задачи, а нахождение решения для группы частных случаев.

Нельзя. Будет всегда компьютер, бракованный, на котором программа не будет работать. На этом факте основано всё лицензирование программного обеспечения. Бракованный компьютер — тоже совокупность аномалий.

По квадратному уравнению имеет смысл рассматривать аномалии только, если от Вас это требуется в задании. И процесс такой длительный:
1. Рассматриваются случаи, когда пользователь ввел уравнение, не являющееся квадратным.
2. Рассматриваются случаи, когда пользователь ввел a,b,c, не являющиеся числами.
3. Рассматриваются случаи, когда пользователь, не умеет запускать программу, пишется инструкция.
4. Рассматриваются случаи, когда пользователь не умеет читать, пишется инструкция с картинками, часто с голосовым помощником.
5. Это именно программа, поэтому можно также составить инструкцию по компиляции, указать различные версии программы для разных стандартов языка.
.
Это все не моя выдумка, так делают, но только, если это действительно нужно.

Бывает другой случай, например, нужно сдать программу, решающую квадратное уравнение, преподавателю и вот здесь нужно сделать минимум, то, что написано в примере, а дальше, только если преподаватель просит.

Нет. Вы не правы.
Про аномалии — я вообще ничего не говорю. Я говорю только про задачу, которую озвучили Вы: решить ax2 + bx + c = 0. Другими словами — найти все возможные ответы при абсолютно любых значениях а, b и с. Без исключений. Не важно — квадратное будет уравнение или линейное, после того, как мы с консоли введем переменные. В этом весь смысл программирования. Сделать универсальное решение, которое будет работать всегда, при любых значениях переменных (аномалии, когда пользователю оторвало руки и он не может ввести переменные с консоли, истекая кровью, я тоже не рассматриваю).
Глупо, имея инструмент, который позволяет решить задачу, не решать её в любых, без исключения, случаях. А ограничивать себя только удобными случаями и тривиальными. Это не программирование получается, а ерунда какая-то, решение частных случаев. «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. »
Вот, корявый, конечно, не оптимальный, но работающий во всех случаях код:

#include
#include
using namespace std;

int main() <
double a, b, c;
cin >> a >> b >> c;
/*(D = b*b minus 4*a*c) — считаем дискриминант*/
double d = (b*b) — 4 * a * c;
double x1, x2, d1;
d1=sqrt(d);/*корень из дискриминанта — заготовка для решения решаемого квадратного уравнения*/
/*1. группируем все исключения — когда решение вообще или через дискриминант невозможно*/
/*2. в каждое исключение сливаем все условия и для этих условий пишем вывод*/
/*3. оставшиеся случаи решаем через дискриминант*/
if ((a==0 && b == 0 ) || ( b==0 && ((c> 0 && a>0) || (c

Про аномалии это я переделал. Лучше говорить аномалии, а не исключения.
Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.
Посмотрите математическую энциклопедию.

Ещё раз повторю: Вы не сможете сделать универсальное решение, которое будет работать всегда.

Ваше решение просто лучше моего, оно не работает, если вместо a, я ввожу rrr или другие символы.

Аномалии про оторванные руки и кровь тоже рассматривают, есть даже задачи и модели математические про ситуацию, когда 0 взял так и случайно стал 1 в памяти ЭВМ. Про глупость, ну а что, так и есть, глупость это нормально. Ваша программа умнее моей.

Это не ерунда, а программирование. Первый этап, который всегда должен происходить, это спецификация (уточнение) задачи. Пишется такая бумага, в которой как раз и есть «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. «.

Вопрос у Вас фактически про спецификацию (уточнение). Те пять пунктов, которые я в предыдущем комментарии написал — совершенно адекватные требования преподавателя, заказчика, сайта с хранилищем программного обеспечения. Часто преподаватели говорят — составить отчёт с инструкциями даже по такой программе как решение квадратного уравнения, это нормально. Про оторванные руки я не писал как раз как про первоочередную задачу.

Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена. Если требуют уточнить, нужно уметь уточнять. Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.

Математической энциклопедии под рукой не нашлось.
«Лучше говорить аномалии, а не исключения.»
Не помню из курса алгебры (в рамках которой изучается решение квадратных уравнений) такого термина — аномалии, но допускаю, что Вы правы и такой математический термин существует и его можно применить к квадратному уравнению.
«Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.»
Прочитал внимательно. «ax2 + bx + c = 0» — где сказано, что а не равен нулю?
«Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена.»
Когда я пытался пропихнуть код, который не учитывает исключений — не приняли, хотя вот текст моего задания:
«На вход вашей программы в стандартном потоке ввода подаются действительные коэффициенты A, B и C уравнения Ax² + Bx + C = 0. Выведите все его различные действительные корни в поток вывода в любом порядке, при этом разделяя корни пробелами. Гарантируется, что хотя бы один из коэффициентов уравнения не равен нулю.»
«Вы не сможете сделать универсальное решение, которое будет работать всегда.» и «Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.»
Позвольте, Вы настаиваете, что невозможно написать код, который будет решать квадратное уравнение при любых действительных a, b и c? Как-то можете теоретически аргументировать? Пока что только не подкрепленные утверждения, не готов принимать их на веру.
При каких действительных значениях а, b и c мой, реально корявый, код не работает?

Страницы математических энциклопедий доступны через Яндекс. Только внимательнее, там есть поясняющие материалы в результатах поиска, не перепутайте.

Квадратное уравнение — алгебраическое уравнение 2-й степени. Общий вид К. у. ax^<2>+bx+c=0, a != 0.

Что такое аномалия?
В тестировании программного обеспечения под аномалией понимается результат, отличный от ожидаемого. Такое поведение может быть результатом документа а также представлений и опыта тестировщиков.

Аномалия может также относиться к проблеме удобства использования, поскольку тестовое программное обеспечение может вести себя в соответствии со спецификацией, но удобство его использования все же можно улучшить. Иногда аномалия также может быть названа дефектом / ошибкой.

Перед тем как разрабатывать программу проводят формальную спецификацию (уточнение) задания.

В информатике формальная спецификация — это математическое описание программной или аппаратной системы, которая может быть реализована в соответствии с этим описанием. Специфицируется, что должна делать система, но не то, как она должна это делать.

Если система огромная — длительное обсуждение, анализ и т.д. Для небольших программ, вот как решение квадратного уравнения, можно на бумаге составить. Вот на этой бумаге пишется задача, ИД — исходные данные, ВД — выходные данные, реакция на аномалии и т.д. В пункте реакция на аномалии рисуется таблица, по крайней мере с двумя столбцами: название аномалии, то что программа будет в этом случае делать.

У Вас в задании слова квадратное как раз нет и аккуратно написано, что подаются только действительные числа. Формальная спецификация выполнена в задании в основном.

Если будут вводить только действительные числа, можно написать работающий код. По такой формальной спецификации можно, я почти уверен, хотя доказательства корректности работы программы трудные.

Нельзя написать универсальное решение, без аномалий, на все случаи жизни. Тот же потенциальный пользователь программы решения квадратного уравнения, школьник, будет тыкать во всю клавиатуру, а не только в цифры.

Приложение для решения квадратных уравнений

Метод Ньютона для решения нелинейных уравнений
В общем, помогите составить программу в Win.Form для решения нелинейных уравнений методом Ньютона.

Метод Ньютона для решения нелинейных уравнений
Помогите написать код для решения уравнений данным методом

Проектирование и выбор решения для реализации (локальное; клиентское приложение)
Вступление для Админов. Куда засунуть эту тему я не нашёл (разделов по проектированию нет (или я.

если в этом же классе.
просто вариант. (попробуй, не проверял)
скинь архив с формой.

Добавлено через 27 минут

Вложения

TheSQR_Equatation.zip (41.0 Кб, 135 просмотров)

Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь или здесь.

Нахождение максимального значения корня среди действительных корней квадратных уравнений
(Написать программу, осуществляющую заданные вычисления с использованием процедур. Вид используемых.

Консольное приложение для решения квадратных уравнений, исправить код
Всем здрасте. Только начал изучать C# и решил написать простенькое консольное приложение для.

Программа для решения квадратных уравнений
В общем надо написать прогу для расчета корней квадратного уравнения. Вот что у меня получилось: .

Программа для решения квадратных уравнений
Здравствуйте! Я написал программу, решающую квадратные уравнения. Все работает. Только есть одна.