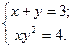SolVE: Local Shared Object Viewer/Editor

(c) 2004 Darron Schall. All rights reserved.

Last updated: Oct. 15, 2004

About

SolVE is a Local Shared Object View/Editor that runs on both Mac OS X and Windows. Coded in Java with IBM’s SWT, SolVE looks and behaves like a native application making transparent to the end user that Java is under the hood.

Currently, SolVE supports the more common basic types but is still in development. The source code has been released under the Common Public License.

Supported Types

Currently, SolVE supports the following data types in local shared object files:

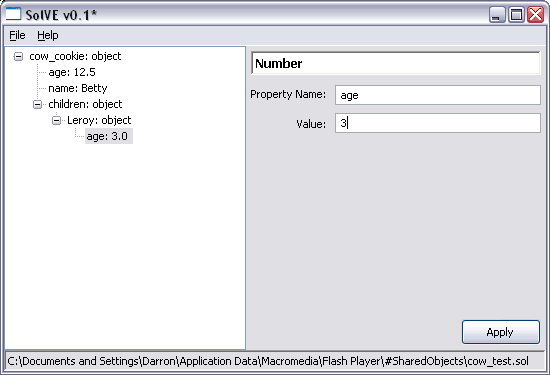
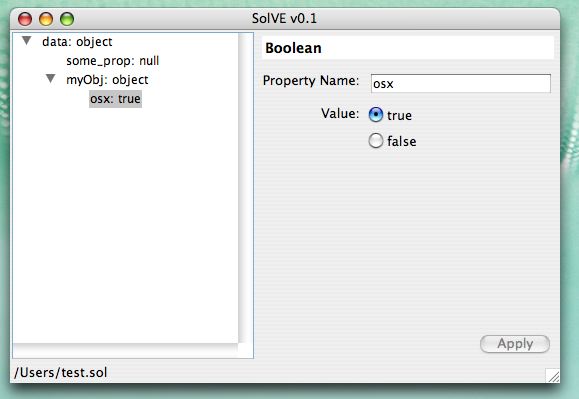
• Number
• Boolean
• String
• Object
• Null
• Undefined
• Array

Features

SolVE is not entirely feature-rich at this point. Still in version .2, the interface allows for basic operations. The main differentiator between SolVE and the other .sol editors (.sol Editor and ASV SOL Viewer/Editor) is that SolVE is a native solution for Mac OS X users and SolVE is available in languages other than English. Never-the-less, here is a basic feature list:

• Runs on Mac OS X and Windows, as long as a JVM at least v1.4 is installed
• Create new .sol files
• Interactive tree display to visually inspect and change contents of a .sol file
• Internationalization support. Please contact me if you’d like to translate SolVE into another language.

Change Log

v0.2 — Oct. 15, 2004 — Darron Schall

• Support for Arrays (Date, XML, etc. coming whenever I get time)
• Fixed a problem with UTF-8 support for String values
• Added French, Bulgarian, and Chinese translations, as well as a menu to change language on the fly. Special thanks to those who translated the resource strings
• Fixed the starting path on Windows for «Open from Player Folder»

v0.1 — Sept. 13, 2004 — Darron Schall

Future Enhancements

The following is a list of features that I plan to implement in SolVE.

• Obviously, support for all of the data types
• Drag and Drop support — simply drag a .sol file onto the application window to open it.
• Drag and Drop support for the data tree — to move nodes around easier
• Better use of SettingsManager — save application state better (window size, window position, last file opened, recent file list, widths for tree/property pane, configurable shortcut keys, etc
• A toolbar needs to be added for shorcuts to open, close, save, etc.
• A «refresh» event item (menu/toolbar) needs to be added
• shorcut keys for the property pane
• add icons/graphics (specifically in the data tree)

Known Issues

Besides not supporting all of the data types for a local shared object, the following is a list of known issues:

• Circular references are not handled correctly. If an object has a member that refers to itself, unexpected results occur
• There doesn’t appear to be a way to set the «start in» folder when opening a file on OS X with SWT. On Windows, there is a menu option to «Open From Player Folder», but I can’t seem to get a file open dialog to start at a specific directory in OS X with SWT.
• The «Open From Player Folder» might only work in Windows 2000 and Windows XP. This will need to be tested on Windows 95/98/ME, and will be corrected (if need be) in a future version.
• When renaming a property, if a property with that name already exists, no error is thrown. Naming two items in a object the same name will produce unexpected results when opening the .sol in Flash
• Long property name aren’t caught correctly yet.

Please send any bug reports to darronschall[at]users[dot]sourceforge[dot]net with a description of the bug, your os version information, and steps to reproduce.

Thanks

Special thanks to Eric Dolecki for graphical support / OS X testing and Jim Cheng for OS X alpha testing.

Huge thanks to the translators:

• Bulgarian — Rostislav Hristov
• Chinese — Deng Jie
• French — zwetan

Donate

If you’d like to support the development of SolVE, please consider giving a donation. I’m building SolVE in my free time that might otherwise be used for contract work. Any support (either monetary, or simple thank you emails) is welcome. Click the paypal button below to donate or send me an email if you find SolVE useful.

ScreenShots

This is SolVE running on my Windows XP machine:

This is SolVE running on Mac OS X 10.3:

License

SolVE is released under the Common Public License.

Disclaimer

THE SOFTWARE IS PROVIDED «AS IS», WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

Basically, SolVE should run just fine. but if it manages to overheat your processor, start a fire, burn the leg of your favorite desk chair, and singe your cat Fluffy’s fur. it’s not my fault. Use at your own risk!

Download

You can find the downloads on the SolVE project page on SourceForge.

If you have trouble getting SolVE to run, please let me know. All of the required libraries are included in the distribution, however SolVE requires Java (1.4 or higher) to run. Mac users can open the zip file and double click the program icon to launch. Windows users can open the zip file and launch SolVE via the executable.

*Note to Windows users: In order to get the Windows XP look, you’ll need to copy javaw.exe.manifest into the same directory where javaw.exe is located (probably something like: C:\Program Files\Java\j2re1.4.2_04\bin)

*Note to Mac Users — I don’t know the minimum OS Requirement for SolVE. I think any version of OS X should work, but I want to say 10.3 is the minimum required. However, I believe Jim Cheng got SolVE to work successfully with 10.2.

Документация

Решите уравнения и неравенства

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Для solve функция в MATLAB ® , смотрите solve .

Синтаксис

Описание

solve(eq, x) возвращает набор всех сложных решений уравнения или неравенства eq относительно x .

solve(eq, x = a..b) возвращает набор всех решений в закрытом интервале Dom::Interval([a, b]) .

solve(eq, vars) решает уравнение для переменных vars .

solve(eqs, x) решает систему eqs для переменной x .

solve(eqs, vars) решает систему eqs из уравнений для переменных vars .

solve функция обеспечивает объединенный интерфейс ко множеству специализированных решателей. Смотрите Выбор Решателя.

Если вы не задаете indeterminates, для которого вы хотите решить уравнение, неравенство или систему, решатель использует набор всего indeterminates. Indeterminates должен быть идентификаторами или индексированными идентификаторами. Вы не можете использовать математические константы, такие как PI, ЭЙЛЕР, и так далее, как indeterminates. Решатель отбрасывает indeterminates, которые появляются только в именах функций или индексах. Смотрите Пример 12.

Если вы задаете список indeterminates, для которого вы хотите решить уравнение, неравенство или систему, решатель сортирует компоненты получившихся векторов решения согласно порядку indeterminates, который вы использовали. Если вы задаете indeterminates как набор, MuPAD ® может изменить порядок indeterminates.

solve(eq, vars) эквивалентно solve([eq], vars) .

Решатель может возвратить следующие типы наборов:

Конечные множества (вводят DOM_SET ).

Символьные вызовы solve .

Нулевые наборы полиномов (вводят RootOf ). Решатель возвращает набор этого типа, если это не может решить уравнение явным образом в терминах радикалов. Решатель также может возвратить этот тип набора, когда вы используете MaxDegree опция.

Относящиеся к теории множеств выражения, такие как «_union» пересечение , и «_minus» .

Символьные вызовы solvelib::Union . Эти вызовы представляют объединения по параметрическим системам наборов.

Отобразите наборы функций (введите Dom::ImageSet ).

Кусочные объекты, в которых каждая ветвь задает набор одного из допустимых типов (вводят piecewise ).

MuPAD может использовать наборы этих типов, исключая интервалы и основные наборы, чтобы представлять наборы векторов (для решений систем). При решении системы MuPAD также может возвратить решение в форме S n ( n — сворачивают декартову степень набора S скаляров). Здесь S является набором любого типа, возвращенного solve .

Для возвращенных наборов решения можно использовать относящиеся к теории множеств операции, такие как intersect объединение , и minus . Кроме того, можно использовать pointwise-заданные арифметические операции, такие как + , * , и так далее. Чтобы извлечь элементы набора, используйте solvelib::getElement функция. Протестировать ли набор решения, возвращенный solve конечно, используйте функциональный solvelib::isFinite . Смотрите пример 2

Для систем решатель возвращает набор векторов или набор списков уравнений. Чтобы указать, что решатель должен возвратить набор векторов, используйте VectorFormat опция. Смотрите Пример 10.

По умолчанию, solve(eq, x) возвращает только решения, сопоставимые со свойствами x . Проигнорировать свойства x , используйте IgnoreProperties опция. Эта опция полезна, когда вы решаете систему уравнений больше чем для одной переменной. Смотрите Пример 13.

Неравенство a или a содержит только, когда обе стороны представляют вещественные числа. В частности, a = b не подразумевает тот a для комплексных чисел.

Можно записать пользовательские области для уравнений специальных типов, и затем перегрузки solve для этих областей. MuPAD использует эту функцию для уравнений повторения и дифференциала. Смотрите ode , ode::solve , и rec страницы справки.

solve функция является символьным решателем. Если вы хотите использовать числовые методы, смотрите numeric::solve страница справки для доступных параметров и примеров.

Если вход содержит числа с плавающей запятой, решатель заменяет их аппроксимированными рациональными значениями. Точность этих приближенных значений зависит от переменной окружения DIGITS . Если solve находит решение, MuPAD внутренне вызывает float функция для того решения, и затем возвращает результат. Если символьный решатель возвращает unevaluated , MuPAD вызывает numeric::solve . Смотрите пример 16.

Если числитель содержит учтенный полином с кратностью, больше, чем 1, решатель не проверяет, что несколько поддерживают нули в знаменателе. Смотрите Пример 17.

Взаимодействия среды

solve реагирует на свойства идентификаторов.

Примеры

Пример 1

Решите следующее уравнение. Как правило, для уравнений с конечным числом решений, решатель возвращает набор DOM_SET ввод:

Решение уравнений и их систем – команда solve

Дата добавления: 2015-06-12 ; просмотров: 4014 ; Нарушение авторских прав

Для решения систем уравнений и одиночных уравнений служит команда

solve(expr1, expr2. exprN, var1, var2. varN). Она возвращает значения переменных varI, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается, что exprI = 0.

Результат может быть возвращен в следующих формах:

для одного уравнения и одной переменной решение возвращается в виде одномерного или многомерного массива ячеек;

при одинаковом числе уравнений и переменных решение возвращается в упорядоченном по именам переменных виде.

Команда solve позволяет найти не только вещественные, но и комплексные решения систем уравнений и одиночных уравнений. Справку по этой команде можно получить, введя команду doc solve.

Решить уравнение x 3 — 1 = 0.

В результате получены три разных значения корня x₁ = 1, x₂ = , x₃ = , которые хранятся соответственно в элементах S(1), S(2), S(3) массива S.

С помощью subs (разд. 7.7) подставим найденные значения корней в выражение x 3 — 1:

Выражение x 3 — 1 принимает значение 0 при подстановке любого из найденных корней, поэтому x₁, x₂, x₃ являются точными корнями уравнения x 3 — 1 = 0.

Команда roots (см. разд. 6.1) нашла бы только приближенные значения корней уравнения x 3 — 1 = 0. В общем случае полиномиальное уравнение степени выше 4 не может иметь точного решения, выраженного с помощью радикалов.

Команда solve позволяет решать уравнения, представленные в аналитическом виде.

Решить квадратное уравнение ax 2 +bx+c = 0.

Команда solve возвратила известные выражения корней x_1,2 = квадратного уравнения ax 2 +bx+c = 0. Точно также можно выразить с помощью радикалов решения кубического уравнения ax 3 +bx 2 +cx+d = 0, хотя эти выражения достаточно сложные.

Решить трансцендентное уравнение x lnx +1 — 1 = 0.

В данном случае solve нашла точные значения корней x₁ = 1, x₂ = e −1 .

Решить трансцендентное уравнение lnx + 3 — x = 0.

Команда solve возвратила значения корней, выраженные через функцию Ламберта.

Команда vpa возвращает приближенные значения этих корней, вычисленные с 20 значащими цифрами:

Каждый из приближенных корней этого уравнения был найден по отдельности в разделе 6.2 с помощью команды fzero. Отметим, что команда solve нашла приближенные значения двух корней одновременно с высокой точностью. При этом не пришлось графически определять интервалы изоляции корней.

Решение любого трансцендентного уравнения, в том числе и тригонометрического (разд. 7.17), достаточно сложная и серьезная проблема. Иногда solve возвращает неверные решения.

Решить трансцендентное уравнение sinx lnsinx +x x — 2 = 0.

Найденное решение неверное, т. к. оно не прошло проверку подстановкой.

Команда solve может возвратить не все решения.

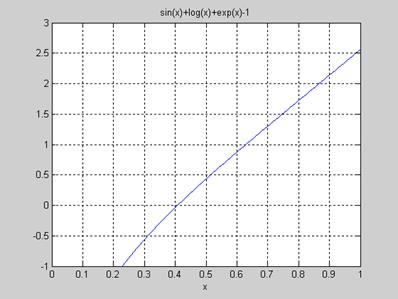
Решить трансцендентное уравнение sinx+lnx+e x — 1 = 0.

Возвратив приближенный комплексный корень уравнения x₁ = -3,0553 — 1,7145i, solve не нашла вещественный корень. С помощью команды ezplot (разд. 7.16) графически определяем, что он находится вблизи значения 0,4 (рис. 7.2):

Вещественный корень со стартовым приближением 0,4 найдем с помощью команды fzero(разд. 6.2):

Итак, приближенное значение вещественного корня x₂=0,4072.

Перейдем теперь к системам уравнений.

Решить систему уравнений

Результатом выполнения команды solve является структура S с полями x и y, каждое из которых содержит символьное представление решения:

Выведем в командное окно содержимое структуры:

Для проверки подставим в выражения Y1 = x+y — 3 и Y2 = xy 2 — 4 вначале первое решение, а затем второе:

>> disp(subs([Y1 Y2],[x y],[S.x(1) S.y(1)])

>> disp(subs([Y1 Y2],[x y],[S.x(2) S.y(2)])

Как видим, найдены точные решения, т. к. выражения Y1 и Y2 при их подстановке обратились в 0.

Команда solve допускает использование символьных переменных в качестве выходных аргументов. Эквивалентное обращение к solve в предыдущем примере имеет вид:

Команда solve позволяет решать системы уравнений, заданные в аналитическом виде.

Решить систему уравнений относительно x, y, z